Chomp ©

300000

روش بازی:

این یک بازی دو نفره است، شما در برابر یک دوست و یا رایانه بازی می‌کنید.
هر بازیکن در نوبت خودش، از صفحه زیر یک شکلات انتخاب می‌کند.
وقتی یک شکلات انتخاب می‌شود، تمامی شکلات‌هایی که در زیر و یا در سمت راست آن شکلات قرار دارند هم از صفحه حذف می‌شوند.

چگونه برنده شویم:

بازیکنی که آخرین شکلات را از قسمت بالا و سمت چپ بردارد، بازی را باخته است.

نوبت بازیکن اول

تعداد کل بازی‌ها: 1072299

تعداد بردهای بازیکن: 81568

تعداد بردهای رایانه: 990709

Access to 'Some food for thought' (SFFT) for the Chomp game can be purchased in the Online Shop

اگر شما فقط می خواهید برای بهتر شدن در بازی به همان سرعتی که ممکن است و سپس پیشبرد به 'بیشتر در مورد چگونگی بازی' >> 'چگونه برای یادگیری از دست دادن موقعیت با کامپیوتر؟'.

غذای زیر برای فکر در دشواری متفاوت است. برخی از آن برای دانش آموزان دبستان مناسب است، به عنوان مثال، آیتم "بیایید چیزی را امتحان کنید". موارد دیگر اثبات های ریاضی را نشان می دهند و سودی که ممکن است از آن ها دریافت کند. این مواد دبیرستانی است. لطفا برای خودتان ببینید چه چیزی مناسب برای شما و یا باشگاه ریاضی مدرسه Caribou خود را.

شما با اولین تفکر برای مدتی قبل از گسترش پاسخ به سوالات بیشترین استفاده را از فعالیت ها دریافت می کنید.

لذت ببر.

برخی از تعاریف برای شروع

بيا يه چيزي رو امتحان کنيم

اجازه دهید با مشکلات آسان، به عنوان یکی از موقعیت های کوچک شروع کنیم. برای ایجاد آنها روی "رایانه: خاموش" کلیک می کنیم. اگر ما پس از آن بر روی کلیک کنید (2،1) تنها یک ردیف از کاشی باقی مانده است.

بازیکن بعدی چه کاری می تواند انجام دهد، منظورم حریف شما است؟
- با کلیک کردن بر روی (1،2) تنها کاشی در (1،1) سمت چپ است ، بنابراین شما از دست داده است.

اجازه دهید ما سپس کلیک کنید 'بازی جدید' و در (3،1) و (2،2) به یک کاشی در ردیف 2 و تمام ردیف 1.

بازیکن بعدی چه کاری می تواند انجام دهد؟
- با کلیک کردن بر روی (1،3) تنها سه کاشی باقی مانده است. ميتوني ببيني که هيچ شانسي نداري؟

بیایید با کلیک بر روی 'بازی جدید' و با کلیک بر روی (3،1) و (2،3).

بازیکن بعدی چه کاری می تواند انجام دهد؟
- حریف شما می تواند بر روی کلیک کنید (1،4). ميتوني ببيني که هيچ شانسي نداري؟

آیا می توانید خلاصه که در کدام موقعیت با کاشی تنها در 2 ردیف شما هیچ شانسی برای برنده شدن در بازی؟
- اگر ردیف بالا تا به یک کاشی بیش از ردیف 2، پس مهم نیست که چه شما انجام دهید، حریف خود را همیشه می تواند یک حرکت به طوری که ردیف بالا تا به یک کاشی بیشتر از ردیف 2. سپس مهم نیست که چه شما انجام دهید، در نهایت شما نیاز به انتخاب (1،1) کاشی و از دست دادن بازی.

اگر یک کاشی کلیک شده است، تمام کاشی های زیر و به سمت راست نیز حذف شده است. این قاعده دارای یک همقارن است؛ یعني کل بازي به صورت زير است: اگر رديف ها و ستون ها را رد و بدل کنيم قانون همان جا مي ماند: تمام كاشي ها به سمت راست تبديل به تمام كاشي هاي زير مي شوند و تمام كاشي هاي زير تبديل به تمام كاشي ها به سمت راست كاشي حذف شده مي شوند. به عبارت دیگر، اگر یک موقعیت را در امتداد خط که از طریق (۱،۱) و (۲،۲) می رود آینه کنیم، آنگاه موقعیت جدید ممکن است متفاوت به نظر بیاید، اما وضعیت مشابهی دارد. حرکت برنده نیز همان حرکت خواهد بود، تنها آینه نیز هست.

موقعیت با 3 کاشی در ردیف اول و 2 کاشی در ردیف دوم ناامید کننده است، همانطور که می دانیم. موقعیت های آینه ای چه کاشی هایی دارند؟
- پس از آینه کاری دارای ۳ کاشی در ستون سمت چپ و ۲ کاشی در ستون دوم است.

ما می دانیم تمام موقعیت های ناامید داشتن کاشی تنها در دو ردیف اول. در مورد تمام موقعیت های ناامید کننده با کاشی تنها در دو ستون اول چه چیزی به ما می گوید؟
- موقعیت های ناامید با کاشی در دو ستون اول کسانی هستند که در آن ستون اول دارای یک کاشی بیشتر از ستون دوم است.

در اینجا موقعیت دیگری بدون شانس است: کلیک کنید 'بازی جدید' و در (4،1)، (2،2) و (1،4).

اگر حریف در این موقعیت حرکت کند پاسخ شما چه است؟
- شما باید مطمئن شوید که پس از حرکت خود را ردیف بالا و ستون اول دوباره از همان طول. با تکرار این الگو، حریف در نهایت مجبور خواهد بود کاشی (۱٬۱) را گرفته و از دست بدهد.

بنابراین، اگر ردیف اول و ستون اول تعداد کاشی های یکسان داشته باشد و کاشی های دیگری وجود ندارد، موقعیت ناامید کننده است. کدام موقعیت ها را می توان به چنین موقعیتی تغییر داد؟
- اگر یک موقعیت دارای همان تعداد ردیف و ستون، مهم نیست که چگونه بسیاری از کاشی در هر جای دیگر وجود دارد: حرکت در (2،2) برگ فقط ردیف اول و ستون اول از طول برابر، ترک حریف هیچ شانسی. بنابراین اگر یک موقعیت دارای همان تعداد کاشی در ردیف بالا به عنوان در ستون سمت چپ و سپس شما در (2،2) بازی و برنده بازی.

برخی از تئوره ها و اثبات ها

برای بازی چامپ به خوبی، باید در مورد برنده شدن و از دست دادن موقعیت ها بداند. یک موقعیت برنده، موقعیتی است که در آن می توان یک برد را اجرا کرد اگر کسی به طور بهینه بازی کند، مهم نیست که طرف مقابل چه می کند. موقعیت از دست دادن است که در آن یکی هیچ شانسی اگر طرف مقابل بازی بهینه است. نقاط زیر چیزی است که یکی در ریاضیات یک تعریف می نامد. در چامپ، موقعیت های باخت و برنده از طریق این ۳ امتیاز تعریف می شوند:
1. اگر تنها یک کاشی باقی مانده است (در گوشه بالا سمت چپ) ، سپس این موقعیت از دست دادن است.
2. یک موقعیت یک موقعیت برنده است اگر حرکت وجود داشته باشد که منجر به یک موقعیت بازنده برای حریف شود.
3. یک موقعیت یک موقعیت بازنده است اگر هر حرکت منجر به یک موقعیت برنده برای حریف شود.
در نگاه اول نقاط فوق ممکن است بی فایده به نظر برسند زیرا موقعیت های برنده با از دست دادن موقعیت ها توضیح داده می شوند و از دست دادن موقعیت ها با کسب موقعیت ها توضیح داده می شود. با این وجود، تعریف بر اساس انجام حرکت ها است و هر دنباله ای از حرکت ها در نهایت منجر به موقعیت کاشی واحد می شود که با توجه به نقطه ۱ یک موقعیت بازنده است.

آیا ممکن است مواضعی وجود داشته باشد که هیچ یک از دو طرف نتونند یک برد را اجرا کنند؟ (دشوار)
- ما یک تئوری کوچک تدوین خواهیم کرد و آن را اثبات خواهیم کرد. اثبات به ما نشان خواهد داد که چگونه برای رسیدن به قدرت بازی کامل. اثبات اثبات توسط القای است که در آن یکی نشان می دهد که بیانیه ای که ما می خواهیم برای اثبات درست است برای یک کاشی و سپس نشان می دهد که اگر آن را برای هر عدد N از کاشی درست است و سپس آن را نیز باید برای یک کاشی بیشتر درست باشد، يعنی N+1 کاشی. از آنجا که این بیانیه برای N=1 کاشی درست است، باید برای N+1=1+1=2 کاشی درست باشد. اما درست بودن برای N=2، پس از آن نیز باید برای N+1=2+1=3 کاشی درست باشد، و مانند آن؛ به طوري که براي هر تعداد كاشي .
- Lemma (theorem small): هر موقعیت یا یک موقعیت برنده یا بازنده است.
- اثبات با القای:
- پایه القایی: اگر موقعیت تنها یک کاشی پس از آن این کاشی در گوشه بالا سمت چپ است و سپس موقعیت از دست دادن با توجه به قاعده Chomp (نشان می دهد که لم درست است اگر تنها N=1 کاشی وجود دارد).
- فرضیه القایی: ما فرض می کنیم که lemma درست است برای تمام موقعیت با تا کاشی N، به عنوان یکی از موقعیت های با 1،2,..., N کاشی یا برنده و یا از دست دادن موقعیت.
- مرحله القایی: ما در حال حاضر می خواهیم نشان دهد که پس از آن نیز تمام موقعیت با کاشی N+1 باید یا از دست دادن و یا برنده موقعیت.
- در P زیر یک موقعیت دلخواه با کاشی های N+1 است. اگر P با یک حرکت کاهش یابد آنگاه موقعیت جدید باید ≤N کاشی داشته باشد، بنابراین یک باخت یا یک موقعیت برنده با توجه به فرضیه القایی است. اگر P را می توان در یک حرکت به یک موقعیت از دست دادن کاهش می یابد و سپس P یک موقعیت برنده است. اگر نه، آنگاه P را می توان در یک حرکت تنها به یک موقعیت برنده کاهش داد. اما اگر یک موقعیت را می توان در حرکت تنها به یک موقعیت برنده کاهش می یابد و سپس P باید یک موقعیت از دست دادن باشد. این ثابت می کند که P (داشتن کاشی های N+1) یا یک برنده یا یک موقعیت بازنده است. این نشان می دهد که تمام موقعیت ها (با N+2,N+3,... کاشی) یا برنده و یا از دست دادن موقعیت.
  
  پایان اثبات ∎
- نظر اضافی: گام القایی روشی را برای تصمیم گیری برای تمام موقعیت ها (تا اندازه ای) فراهم می کند که آیا در حال برنده شدن یا از دست دادن موقعیت ها هستند. با موارد زیر تعریف می شود:
  
  یکی با N=1 شروع می شود و برچسب هایی که موقعیت را به عنوان یک موقعیت از دست دادن قرار می دهند. یکی پس از آن تعیین وضعیت تمام موقعیت با 2 کاشی، سپس با 3 کاشی و مانند آن، هر بار با استفاده از دانش از وضعیت موقعیت های کوچکتر، و اضافه کردن موقعیت از دست دادن تازه پیدا شده به لیست موقعیت از دست دادن شناخته شده است.
- این یک راه بسیار کارآمد برای پیدا کردن تمام موقعیت های برنده و از دست دادن تا برخی از اندازه است. با بزرگتر شدن اعداد در اندازه، یک برنامه کامپیوتری مفید خواهد بود. مواد لازم به قرار زیر است:
  - روشی که می تواند به طور کارآمد تمام موقعیت های N کاشی از دانستن تمام موقعیت های کمتر از N کاشی ایجاد
  - رویه ای که می تواند به طور کارآمد بررسی کند که آیا یک موقعیت را می توان به موقعیت داده شده دیگری کاهش داد یا نه.
  ما آن را به شما بذاریم تا بیشتر به آن فکر کنید و شاید چنین برنامه کامپیوتری بنویسید.

چند موقعیت باخت و برنده دقیقا 2 کاشی دارند؟
- تنها دو موقعیت ممکن است که دقیقا 2 کاشی، 2 کاشی در ردیف بالا، و یا دو کاشی در امتداد ستون سمت چپ وجود دارد. هر دوی این ها در حال کسب هستند.

چند موقعیت باخت و برنده دقیقا 3 کاشی دارند؟
- 3 مجموع موقعیت ممکن است که دقیقا 3 کاشی وجود دارد. آن ها از ۲ برنده، و ۱ موقعیت باخت تشکیل شده اند. ميتوني بفهمي اونا کدوم موقعيت هستن؟

چند موقعیت باخت و برنده دقیقا 4 کاشی دارند؟
- 5 موقعیت ممکن است که دقیقا 4 کاشی وجود دارد. همه این ها برنده ها هستند.

چند موقعیت باخت و برنده دقیقا 5 کاشی دارند؟
- 7 کل موقعیت ممکن است که دقیقا 5 کاشی وجود دارد. از این ها ۳ در حال از دست دادن موقعیت ها و ۴ برنده هستند. ميتوني بفهمي اونا کدوم يکي هستن؟

آیا موقعیت های مستطیل شکل برنده هستند یا موقعیت ها را از دست می دهند؟
- لما زیر به این سوال پاسخ می دهد. اثبات اثبات وجود است. تنها وجود یک حرکت برنده را ثابت خواهد کرد بدون اینکه نشان دهد این حرکت چه چیزی است. با این وجود، دانستن لما برای بازی شما مفید است همانطور که در زیر توضیح داده شده است.
- Lemma: تمام موقعیت های مستطیلی به جز موقعیت ۱ کاشی، موقعیت های برنده هستند.
- اثبات: برای نشان دادن این درست است ما باید دو مورد ممکن را در نظر بفهمیم:
  1. از بین بردن کاشی در گوشه پایین سمت راست هیئت مدیره یک حرکت برنده است.
  2. از بین بردن کاشی در گوشه پایین سمت راست یک حرکت برنده نیست.
- اگر مورد ۱ درست باشد، پس این بدان معناست که مستطیل یک موقعیت برنده است، و این از لم حمایت می کند.
- اگر مورد 1 درست نباشد، پس باید مورد 2 را در نظر ب گرفت. با توجه به اثبات ما قبلا انجام داد، موقعیت ناشی از از بین بردن کاشی در گوشه سمت راست پایین تر پس از آن باید یک موقعیت برنده، که بدان معنی است که آن را باید یک حرکت برنده است که وجود دارد داشته باشد. اما چون هر حرکت در مستطیل، کاشی را در گوشه پایین سمت راست حذف می کند، موقعیت بازنده ناشی از حرکت دوم (حرکت برنده) همان است که آیا حرکت برنده پس از حرکت گوشه انجام می شود یا به جای حرکت گوشه. این بدان معنی است که حرکت برنده می توانست فوراً انجام شود و به این ترتیب ثابت کند که یک حرکت برنده برای موقعیت مستطیل شکل وجود دارد.
- پایان اثبات ∎
- نظرات اضافی: اگر چه lemma به ما نمی گوید چه حرکت برنده است، آن را در حال حاضر مفید است بدانید که موقعیت های مستطیل شکل در حال برنده شدن موقعیت. بنابراین یکی نباید حرکت کند که یک موقعیت مستطیل شکل ایجاد کند (به جز موقعیت ۱x۱).

آیا می توانید برای هر هیئت مدیره مربع تعیین چه حرکت برنده است؟
- برای تمام مربع های اندازه >1 تنها حرکت برنده در (2،2) است.

برای کدام موقعیت ها شبیه به یک مربع همان حرکت یک حرکت برنده است؟
- حرکت (۲٬۲) نیز یک حرکت برنده برای هر موقعیتی است که ردیف اول و ستون اول طول یکسانی داشته باشد.

آیا یک موقعیت می تواند بیش از یک حرکت برنده داشته باشد؟
- بله یک موقعیت می تواند بیشتر پس از آن یک حرکت برنده داشته باشد. موقعیت زیر را در نظر بگیرید:
  
  ###
  ##
  #
  
  این موقعیت هیئت مدیره دارای ۳ حرکت برد مختلف است که می توان آن ها را انجام داد. ميتوني مشخص کني اونا چي هستن؟

بیشتر در مورد چگونگی بازی

استراتژی کلی برای برنده شدن در Chomp این است که ایجاد موقعیت از دست دادن برای حریف خود را به طوری که آنها هیچ شانسی. ما همچنین می خواهیم برای جلوگیری از ایجاد موقعیت های برنده است که حریف می تواند به از دست دادن موقعیت برای ما تبدیل.

کلید برنده شدن این است که بدانید به عنوان بسیاری از موقعیت های از دست دادن که ممکن است، و برای تشخیص چگونگی ایجاد یکی قبل از حریف خود را انجام می دهد. بیایید هیئت مدیره ممکن زیر را در نظر بیم که یک موقعیت از دست دادن شناخته شده است:

#######
###
###
#
#
شکل ۱
همه موقعیت هایی که می توان در یک حرکت به این موقعیت از دست دادن تبدیل کرد چه هستند؟
- موقعیت از دست دادن بالا می تواند از هر حرکت مشخص شده با + زیر نتیجه:
  
  #######+
  ###
  ###
  #
  # #######
  ###+
  ###
  #
  # #######
  ###
  ###
  #+
  # #######
  ###
  ###
  #
  #
  +
  
  شکل ۲
  
  این حرکت ها همگی در گوشه های بریده شده قرار دارند. هر گونه حرکت + نیز قطع کاشی است که ممکن است در تصاویر زیر ظاهر می شود با ?:
- #######+?
  ###
  ###
  #
  # #######
  ###+???
  ###????
  #
  # #######
  ###
  ###
  #+?
  #?? #######
  ###
  ###
  #
  #
  +
  ?
  
  شکل 3
- کاشی + لازم است ، و ? کاشی اختیاری هستند. در موقعیت برنده چپ، ردیف بالا را می توان خودسرانه به سمت راست با '?'بیشتر گسترش داد، و در موقعیت برنده راست، ستون اول را می توان خودسرانه به پایین با '؟'. همه این ها نیز برنده هستند. اگر قرار باشد در چنین موقعیتی حرکتی انجام بدهیم، یک + کاشی می گیریم، و بنابراین همه ? کاشی متصل نیز حذف خواهد شد، و در نتیجه موقعیت از دست دادن ما با آغاز شده است.

آیا موقعیت های برنده تر یا بیشتر از دست دادن وجود دارد؟
- برای هر موقعیت از دست دادن بی نهایت بسیاری از موقعیت است که می تواند به این موقعیت از دست دادن توسط یک حرکت تبدیل وجود دارد. بنابراین همه آن های بی نهایت بسیاری در حال کسب هستند.
- بنابراین موقعیت های برنده بسیار بیشتری نسبت به از دست دادن موقعیت ها وجود دارد. بنابراین ، آن را موثر ترین به یاد داشته باشید به عنوان بسیاری از موقعیت های از دست دادن که ممکن است ، تمام موقعیت های دیگر برنده موقعیت.

یک لیست از از دست دادن موقعیت است که شما می دانید، و برای هر موقعیت نوشتن تمام موقعیت های برنده مربوطه و چگونه آنها را تشخیص
- مثال زیر نشان می دهد که منظور ما چیست:
- همانطور که قبلا نشان داده شده است، هنگامی که موقعیت تنها 2 ردیف، و ردیف بالا دارای یک کاشی بیش از ردیف دوم، از این موقعیت از دست دادن است، همانطور که در زیر نشان داده شده است:
- #####
  ####
- با در نظر گرفتن این موقعیت از دست دادن شناخته شده، ما می توانیم تعیین کنیم که موقعیت های برنده مربوطه هستند:
- #####+?
  #### #####
  ####+ #####
  ####
  +???
  ????
- در موقعیت سمت چپ، می تواند هر تعداد وجود داشته باشد؟ به سمت راست ردیف بالا، و در موقعیت مناسب، می تواند هر تعداد از ردیف وجود داشته باشد؟ زیر. ما می توانیم در کلمات خلاصه چگونه برای تشخیص این موقعیت های برنده (که شما باید برای بازی خود را به یاد داشته باشید):
- - موقعیت یک موقعیت برنده است که کاهش می دهد به
    #####
    ####
  - - اگر یا موقعیت فقط دو ردیف داشته باشد، و ردیف اول دقیقاً یک کاشی طولانی تر نیست آنگاه ردیف دوم، یا
  - - اگر موقعیت بیش از دو ردیف داشته باشد، و ردیف اول دقیقاً یک کاشی طولانی تر باشد آنگاه ردیف دوم.
- اما بیشتر برای فکر کردن به آن نیز وجود دارد. ما نه تنها می خواهیم در چنین های برنده ای درست بازی کنیم، بلکه می خواهیم از انجام حرکتی که چنین موقعیت های برنده ای را ایجاد می کند، اجتناب کنیم. این بدان معنی است که ما نباید یک حرکت که در آن تنها دو ردیف باقی می ماند، و یا جایی که ردیف دوم دقیقا یک کاشی کمتر پس از آن ردیف اول است.
- برای خلاصه کردن، ما می خواهیم موقعیت های از دست دادن ایجاد کنیم، اما همچنین می خواهیم از ایجاد موقعیت هایی که یک حرکت به دور از یک موقعیت بازنده است، اجتناب کنیم.
- چیز دیگری که باید به آن توجه داشت: با توجه به آینه ای که قبلاً گفته شد، می توان تمام نظرات فوق را به سادگی با جایگزین کردن کلمه «ردیف» با کلمه «ستون» تکرار کرد.
- این است که به شما برای جمع آوری موقعیت های از دست دادن بیشتر و موقعیت های برنده مربوطه خود را که یک حرکت دور سمت چپ.

ايلي مجبور باشي توي يه موقعيت بازنده بازي کني چي؟
- اگر شما متوجه شوید که شما باید یک حرکت در یک موقعیت از دست دادن، پس در تئوری شما هیچ شانسی ندارد. همه شما می توانید انجام دهید این است که امیدواریم که حریف خود را نمی داند تمام حرکت برنده برای موقعیت است که شما می توانید با حرکت بعدی خود را ایجاد کنید. کاری که می توانستید بکنید این است که فقط یک کاشی واحد را از گوشه ای حذف کنید. این می دهد حریف خود را یک موقعیت حاصل از اندازه حداکثر, و آن را باعث می شود آن را دشوار تر برای حریف خود را به دانستن حرکت برنده مربوطه.

اگر شما هیچ موقعیت از دست دادن نمی دانم چه؟
- یکی باید برای انجام آنچه به عنوان یک جستجوی درخت کامل شناخته می شود. بازیکن اول با حدس زدن یک حرکت شروع می شود، سپس بازیکن دوم یک حرکت را حدس می بزند و همین طور تا زمانی که یک بازیکن، بگوید بازیکن A، برنده می شود. سپس بازیکن B مجاز به تغییر آخرین حرکت آنها ساخته شده است و آن را به نوبه خود بازیکن A بعدی است. اگر در یک موقعیت بازیکن بازی بعدی، می گویند B، اجرا می شود از حرکت به دلیل تمام حرکت منجر به باخت، پس از آن این یک موقعیت از دست دادن است، و بازیکن B می تواند آخرین حرکت انجام شده قبل از رسیدن به این موقعیت از دست دادن را تغییر دهید.
- این 'جستجوی درخت' ادامه می یابد تا زمانی که مشخص شود که آیا موقعیت شروع یک موقعیت از دست دادن است یا کدام حرکت بازیکن ۱ آن را به یک موقعیت از دست دادن تبدیل می کند.
- این می تواند یک فرایند بسیار طولانی اگر کسی تلاش می کند تا آن را در هیئت مدیره اولیه با کاشی های بسیاری انجام دهد. با این حال، هر چه موقعیت های از دست دادن بیشتری بدانیم توالی های حرکت ها قبل از رسیدن به چنین موقعیتی کوتاه تر هستند و به این ترتیب کل جستجو بسیار سریع تر است. اگر ما می دانستیم که همه حاوی موقعیت های از دست دادن، پس یا موقعیت شروع به عنوان یک موقعیت از دست دادن به رسمیت شناخته می شود، و یا تنها یک حرکت لازم خواهد بود برای کاهش آن را به یک موقعیت از دست دادن.

چگونه برای یادگیری از دست دادن موقعیت با کامپیوتر؟
- در سطح دشواری 'بسیار سخت' و موقعیت های بزرگتر از 8 x 15 کامپیوتر بازی کاملا به طوری که هر موقعیت است که نتایج حاصل از حرکت کامپیوتر از دست دادن پستی است! یکی باید با تخته های بسیار کوچک شروع و بازی در برابر کامپیوتر در سطح 'بسیار سخت' و یادگیری تمام موقعیت هایی که کامپیوتر تولید می کند. برای هر موقعیت از جمله فکر می کنم که چگونه هر یک از حرکت های خود را توسط کامپیوتر تبدیل آن را دوباره به یک موقعیت از دست دادن کوچکتر پاسخ داده می شود. برای هر موقعیت از دست دادن نیز موقعیت آینه ای (ردیف <--> ستون) یک موقعیت از دست دادن است.
- اولین حرکت مطلوب چه چیزی است؟
  - در مسابقه موقعیت شروع مستطیلی از آبله ها خواهد بود. همان طور که پیش از این ثابت شد، مستطیل یک موقعیت برنده است، اما اولین حرکت تغییر آن به یک موقعیت بازنده برای حریف چه چیزی است؟ ما زودتر یاد گرفتیم که حرکت بهینه برای یک مربع کاشی (۲٬۲) است اما اگر مستطیل مربع ن باشد چه؟
  - به سادگی به سطح دشواری 'بسیار سخت' تغییر و اجازه دهید کامپیوتر را به حرکت اول. تا زمانی که مستطیل بزرگتر از 8x15 نیست، کامپیوتر به صورت بهینه بازی می کند و اولین حرکت کامل را نشان خواهد داد. سعی کنید اندازه مستطیل های مختلف و به یاد داشته باشید حرکت اول مطلوب به دلیل بازی کامپیوتر در روزهای مسابقه در دسترس نخواهد بود :).
- به زودی شما در سطح دشواری آسان و متوسط بی نظیر خواهد بود.

آیا خانواده های بی نهایت از دست دادن موقعیت وجود دارد؟
- ما از قبل با این دو خانواده از دست دادن موقعیت ها آشنا شدیم. N هر یک از اینت مثبت است.
- در اینجا بیشتر:

پخش کننده کامپیوتر چگونه کار می کند؟

برخی از ریاضی بیشتر در اطراف Chomp (سطح دبیرستان)

نظرات زیر کمکی به قوی تر شدن در Chomp نخواهد کرد، اما آنها برخی از حقایق جالب را فراهم خواهد کرد و به ما فرصت دیگری برای تمرین اثبات توسط القای.

چند موقعیت مختلف، از جمله تخته خالی، به یک مستطیل با ردیف های P و ستون های Q جا می گیرند؟
- اگر مستطیل خالی را شامل شود، می توانیم تعداد کل موقعیت های ممکن را با استفاده از فرمول زیر محاسبه کنیم: \[\frac{(P+Q)!}{P!Q!}\]آیا می توانید آن عدد را برای P و Q کوچک محاسبه کنید، و تأیید کنید که درست است؟
- مشتق اول یک فرمول بازگشتی
  - اجازه دهید f(P,Q) تعداد موقعیت ها در مستطیل اندازه PxQ باشد. یک مشاهده مهم این است که تمام موقعیت ها شکل یک راه پله را دارند، جایی که هر ردیف در بیشتر کاشی ها به اندازه ردیف بالا دارد، اما نه بیشتر.
  - اجازه می دهد تا برای اولین بار با راه ما می توانیم تمام این راه پله ها را نشان می دهد شروع می شود. یکی از راه های ایجاد راه پله به راحتی این است که در گوشه پایین سمت چپ تخته شروع کنید، و یا به سمت راست یا بالا حرکت کنید. می توان به انجام این حرکت های درست و بالا تا زمانی که آنها را به گوشه سمت راست بالا از هیئت مدیره ادامه دهد. ما از این به عنوان مسیری که برای رسیدن از (P,0) به (0,Q) در پیش گرفتیم، نام خواهیم برد.
  - تعداد موقعیت ها همان تعداد مسیرها از (P,0) به (0,Q) است، تا زمانی که یکی تنها اجازه حرکت به بالا یا سمت راست را داشته باشد. عدد f(P,Q+1) مسیرهایی که از (P,0) به (0,Q+1) می روند، عدد f(P,Q) مسیرهایی است که از (P,0) به (P,0) می روند 0,Q), and then to (0,Q+1) + the number f(P-1,Q) of paths to get from (P,0) to (1,Q), and then to (1, Q+1) و (0,Q+1), و مانند آن. فرمول متناظر به این قرار است:\[f(P,Q+1) = f(P,Q) + f(P-1,Q) + f(P-2,Q) + \ldots + f(1,Q) + f(0,Q)\]
  - اکنون این فرمول را می گیریم و P را با P + 1 جایگزین می کنیم. اگر P + 1 را به جای P به فرمول وصل کنیم، موارد زیر را بدست می آوریم: \[f(P+1,Q+1) = f(P+1,Q) + f(P,Q) + f(P-1,Q) + \ldots + f(0,Q)\] \[f(P+1,Q+1) = f(P+1,Q) + f(P,Q+1)\]از این مشتق جدید می توانیم فرمول را تعیین کنیم \(f(P,Q) = f(P,Q-1) + f(P-1,Q)\) آن \(f(P,0) = 1\) و \(f(0,Q) = 1\).
- یک مشتق جایگزین از یک فرمول بازگشتی
  - اغلب راه های متعددی برای شمارش در مشکلات ترکیب وجود دارد. مشتق زیر راهی متفاوت و ظریف تر برای مشتق گیری فرمول فراهم خواهد کرد.
  - ما از همان بازنمایی که قبلاً استفاده کرده بودیم استفاده خواهیم کرد، جایی که می خواهیم تعداد کل مسیرهایی را که ما را از (P,0) به (0,Q) می گیرند، پیدا کنیم. ما می توانیم این مسیرها را به دو گروه سازماندهی کنیم.
  - مسیرهایی که با اولین حرکت رفتن به سمت راست از (P,0) به (P,1) شروع می شوند. می دانیم که در این گروه مجموعاً مسیرهای f(P,Q-1) از (P,1) تا (0,Q) خواهیم داشت. ما این را می دانیم زیرا مستطیل باقی مانده پس از حرکت یکی به سمت راست از اندازه P x (Q-1) است.
  - گروه دیگر مسیرهایی هستند که با اولین حرکت بالا رفتن یک حرکت از (P,0) به (P-1,0) شروع می شوند. در این گروه می دانیم که مسیرهای کل f(P-1,Q) وجود دارد، چرا که مستطیل حاصل از اندازه (P-1) x Q خواهد بود.
  - بنابراین از آنجا که هر مسیر ممکن در یکی از این دو گروه قرار خواهد گرفت، تعداد کل مسیرها مجموع این گروه ها است. این به ما همان فرمول را می دهد \(f(P,Q) = f(P,Q-1) + f(P-1,Q)\).
- مشتق یک فرمول صریح
  - به جای شروع مسیرها از گوشه پایین سمت راست، بیایید مستطیل را بچررخیم تا نقطه (P,0) در بالا قرار گیرد. هم اکنون می توانیم مسیرها را با نمودار زیر تجسم کنیم:
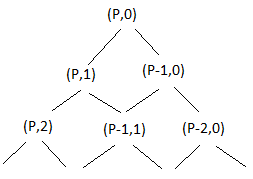
  - این نوع نمودار به عنوان یک درخت شناخته می شود. این الگو در تکرار نگه دارید تا زمانی که ما از (P،0) به (0،Q) سفر کرده اند. هنگامی که این اتفاق می افتد، درخت شامل هر مسیر ممکن است یکی می تواند در سراسر هیئت مدیره را.
  - تعداد راه های رسیدن از بالا (P,1) به یک گره (I,J) در این درخت تعداد راه های رسیدن به (I-1,J) است، و سپس پایین رفتن درست به (I,J)، به علاوه تعداد راه های رسیدن به (I,J-1)، و سپس پایین رفتن به سمت چپ به (I,J). به عبارت دیگر این عدد در مثلث پاسکال است.
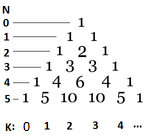
  - هر عدد در مثلث پاسکال مجموع دو عدد بالا است. اعداد در ستون سمت چپ در حال شمارش ردیف های هیئت مدیره هستند که از ۰ با یک تخته خالی شروع می شود. اعداد زیر مثلث نشان دهنده موقعیت از سمت چپ است، همچنین از ۰ شروع می شود. عدد در ردیف N'th در موقعیت K برابر است با \({N \choose K} = \frac{N!}{(N-K)!K!}\).
  - ما می خواهیم عدد f(p,q) را پیدا کنیم که تعداد راه های دریافت از (P,0) به (0,Q) است. برای انجام این کار یکی باید از بالا P بار پایین سمت راست و Q بار پایین سمت چپ بروید. با استفاده از ساختار درختی که قبلاً تعریف کرده بودیم، این همان رفتن از (۰٬۰) به (P,Q) رفتن تنها چپ و راست در درخت است.
  - با این حال، این باعث می شود که ما گام های P+Q را بسازیم، بنابراین در ردیف P+Q در درخت هستیم. از آنجا که ما می دانیم که ما نقل مکان کرد Q بار به سمت راست، شماره در مثلث پاسکال در این موقعیت است \({P+Q \choose Q} = \frac{(P+Q)!}{P!Q!}\).
- اثبات فرمول صریح توسط القای
  - قرار است نشان دهیم که فرمول های زیر معادل هستند. \[f(P,Q) = \begin{cases}1 & for & P=0 \\1 & for & Q=0 \\f(P,Q-1) + f(P-1,Q) & for & \text{P>0 and Q>0}\end{cases} = \Bigg\{{P+Q \choose Q} = \frac{(P+Q)!}{P!Q!}\]
  - پایه القایی: ما در حال حاضر می دانیم که f(0,0) = 1 توسط تعریف فرمول. اگر P=0 و Q=0 را به فرمول وصل کنیم، بدست می آوریم \(\frac{(0+0)!}{0!0!} = \frac{0!}{1} = 1\). این نشان می دهد که فرمول های پایه معادل هستند، که پایه القایی را به پایان می رسد.
  - فرضیه القایی: فرض کنیم که فرمول ها برای تمام مقادیر P,Q با P+Q = N معادل هستند.
  - مرحله القایی: با استفاده از فرضیه القایی، هم ارزی را برای تمام مقادیر P,Q با P+Q=N+1 ثابت می کنیم. برای هر مقادیر P,Q با P+Q=N+1، ما ۳ مورد داریم:
  - مورد 1:
  - مورد 2:
  - مورد 3: \(P,Q > 0\) \[ \begin{align} f(P,Q) &= f(P,Q-1) + f(P-1,Q)\qquad\qquad (+)\\ &= \frac{(P+Q-1)!}{P!(Q-1)!} + \frac{(P-1+Q)!}{(P-1)!Q!}\\ &= \frac{(P+Q-1)!Q}{P!(Q-1)!Q} + \frac{(P-1+Q)!P}{(P-1)!PQ!}\\ &= \frac{(P+Q-1)!}{P!Q!} (Q+P)\\ &= \frac{(P+Q)!}{P!Q!} \end{align} \]
  - (+): اگر P + Q = N + 1، آنگاه P + Q-1 = N، به عبارتی با فرضیه القایی.
    f(P,Q-1) = \(\frac{(P+(Q-1))!}{(P!(Q-1)!)}\), و به طور مشابه برای f(P-1, Q)
  - این نشان می دهد که دو فرمول برای f(P,Q معادل هستند.
  - پايان اثبات . ∎

چند موقعیت مختلف دارای ردیف های P و ستون های Q هستند؟
- به سادگی می توان از فرمول یکسان برای تمام موقعیت های اتصالات به یک مستطیل با ردیف های P-1 و ستون های Q-1 استفاده کرد که f(P-1,Q-1) است.

آیا موقعیت های برنده تر یا بیشتر از دست دادن وجود دارد؟

# of tiles	# of positions	# of lose positions	٪ از دست دادن موقعیت
20	627	42	6.69
30	5604	220	3.92
40	37338	1022	2.73
50	204226	4976	2.43
60	966467	20106	2.08
70	4087968	76688	1.87
80	15796476	270142	1.71
90	56634173	897964	1.58

فرضیه ای از کاریبو

پیش از این نشان داده بودیم که هر موقعیت یا یک برد است یا یک موقعیت بازنده. اثبات به ما یک روش مستقیم برای تعیین گام به گام برای تمام موقعیت ها که آیا آنها در حال از دست دادن و یا برنده شدن. چیزی که خاص بود این است که این روش نیازی به هیچ جستجو (تلاش کردن حرکت ها) نداشت. این ما را به یاد 'سیو از Eratosthenes' برای تعیین تمام اعداد اول تا برخی از اندازه.

دفعات بازدید : در مورد Sieve از Eratosthenes ، به عنوان مثال در اینترنت
- برای پیدا کردن تمام اعداد اول تا اندازه N²، که در آن N برخی از تعداد کامل است، یکی از موارد زیر را انجام دهد:
- - A: Start with the prime number p=2.
  - ب: عبور از تمام چند برابر p تا N².
  - ج: پیدا کردن بزرگترین عدد بعدی > p است که هنوز عبور نکرده است. اگر آن عدد > باشد، آنگاه الگوریتم متوقف می شود. در غیر این صورت با این عدد p تماس بگیرید و با گام B ادامه پیدا کنید.
- تمام اعداد تا N² که از هم عبور نمی کنند همه اعداد اول < N^{2 هستند}. می توان شبیه سازی این الگوریتم را بر روی https://en.wikipedia.org/wiki/Sieve_of_Eratosthenes

این قیاس الهام بخش ما بود که به شباهت های بیشتری بین اعداد اول و از دست دادن موقعیت ها فکر کنیم. منجر به فرضیه ای برای از دست دادن موقعیت هایی شد که شبیه به 'تئوری اعداد نخست' است. در اینجا جزئیات.

جدول: قیاس بین از دست دادن موقعیت در chomp و اعداد نخست:

شماره‌ها	چامپ
اعداد کامل بی نهایت زیادی وجود دارد.	موقعیت های بی نهایت چامپ وجود دارد.
اعداد اول و اعداد فاکتوری قابل فاکتوری وجود دارد.	موقعیت های از دست دادن و کسب موقعیت وجود دارد.
اعداد اول بی نهایت زیادی وجود دارد.	بی نهایت بسیاری از موقعیت های از دست دادن وجود دارد.
یک عدد فاکتوریزا محصول یک عدد اول و یک عدد است.	موقعیت برنده مجموع یک موقعیت بازنده و یک موقعیت است (زیرا آنچه در یک حرکت قطع می شود شکل پلکان دارد، و بنابراین یک موقعیت است).
هنگامی که یک عدد اول شناخته شده است، یکی می داند فورا بی نهایت بسیاری از اعداد فاکتوریز (تمام چند برابر از عدد اول).	هنگامی که یک موقعیت از دست دادن شناخته شده است، یکی می داند فورا بی نهایت بسیاری از موقعیت های برنده (تمام موقعیت های ناشی از پر کردن مستطیل گوشه، از جمله کسانی که آنهایی که بی نهایت طولانی در امتداد ردیف بالا و ستون سمت چپ).
یک عدد بزرگ بسیار بیشتر احتمال دارد که توسط یک عدد نخست کوچک قابل تفرقه باشد تا یک عدد نخست بزرگ.	یک موقعیت بزرگ بسیار بیشتر احتمال دارد که به یک موقعیت از دست دادن کوچک کاهش یابد تا به یک موقعیت از دست دادن بزرگ.
برای تعیین اینکه آیا یک عدد N یک عدد اول است یا نه، دانستن تمام اعداد نخست P تا ریشه مربع N بسیار کارآمد است. سپس می توان بررسی کرد که آیا N را می توان با تقسیم به P کاهش داد یا خیر، به عنوان یکی از تقسیمات آزمایشی N / P.	برای تعیین اینکه آیا یک موقعیت P یک موقعیت از دست دادن است، لازم است بدانید که تمام موقعیت های از دست دادن L که در P موجود است. سپس می توان بررسی کرد که آیا P را می توان در یک حرکت به L کاهش داد یا نه.
'Sieve of Eratosthenes' یک راه کارآمد برای تعیین تمام اعداد نخست تا برخی از اعداد N است، بلکه برای بررسی اینکه آیا یک عدد داده شده یک عدد نخست است یا نه. این الگوریتم در بالا شرح داده شده است.	به طور مشابه به 'Sieve از Eratosthenes' یکی با موقعیت از دست دادن شروع می شود {1}، و عبور از تمام موقعیت های برنده است که به آن موقعیت از دست دادن در یک حرکت را کاهش می دهد. یکی پس از آن بازرسی تمام موقعیت با یک کاشی بیشتر. تمام موقعیت هایی که از آن عبور نمی کنند در حال از دست دادن موقعیت ها هستند.
ناکارآمدی باقی مانده از الگوریتم sieve شامل عبور از اعداد فاکتوریز به طور مکرر است.	ناکارآمدی باقی مانده از الگوریتم sieve شامل عبور از موقعیت های برنده بارها و بارها است.
چگالی اعداد نخست با اندازه آن ها کاهش می یابد؛ i.e. نسبت (# از اعداد اول تا برخی از تعداد کل N) / N کاهش می یابد به عنوان N افزایش می یابد.	تراکم از دست دادن موقعیت ها با اندازه آنها کاهش می یابد؛ i.e. نسبت (# از دست دادن موقعیت با تا N کاشی) / (# از همه موقعیت با N کاشی) کاهش می یابد به عنوان N افزایش می یابد. (چالش: فرمول وابستگی این نسبت به N چگونه است و چگونه آن را با فرمول برای چگالی اعداد نخست مقایسه می کند؟).
Theorem prime number: (# of primes ≤ N) / (N / log(N)) → 1 as N → infinity.	فرضیه تمثیلی: (# از دست دادن موقعیت با کاشی N) / ((# از موقعیت با کاشی N) / ورود به سیستم (# از موقعیت با کاشی N)) → 0.283... به عنوان N → بی نهایت.

جدول: تفاوت بین از دست دادن موقعیت در Chomp و اعداد اول:

شماره‌ها	چامپ
مجموعه تمام اعداد یک مجموعه کاملاً سفارش داده شده است؛ يعني بين هر دو عدد، يکي ميدونه کدوم بزرگتره.	مجموعه تمام موقعیت های Chomp یک مجموعه تا حدی سفارش داده شده است. موقعیت ها را می توان به طور کامل در موقعیت های دیگر موجود است، اما نیاز ندارد.
عملیات کاهش یک عدد به یکی از عوامل نخست آن تقسیم است.	عملیات برای کاهش موقعیت به موقعیت از دست دادن تفریق کاشی است.
یک عدد را می توان به صورت یک بخش خط بر روی یک خط عدد یک بعدی تجسم کرد.	یک موقعیت از طریق فهرستی از اعداد مرتب شده بر اساس اندازه تعریف می شود و به این ترتیب یک شیء دوD است.

باز کردن سوالات:

آیا فرضیه (# از دست دادن موقعیت با N کاشی) / ((# از موقعیت با کاشی N) / ورود به سیستم (# از موقعیت با کاشی N)) → 0.283... همانطور که N → بی نهایت درست است؟

ميتوني ثابتش کني؟ (ما هنوز نمی توانیم :-) )

نسخه های مختلف Chomp

بازی چامپ که در بالا انجام شد نسخه ای از چامپ دو بعدی است. یعنی تخته تنها ۲ بعدی است، دارای عرض و ارتفاع است.

آیا می توانید یک نسخه از Chomp سه بعدی تصور کنید؟
- ساده ترین راه برای تصور اضافه کردن بعد جدید به بازی با اضافه کردن بعد سوم به تخته است. به جای اینکه فقط یک عرض و ارتفاع باشد، تخته جدید طول، عرض و ارتفاع خواهد داشت. اگر کسی مکعب های کمی برای بازی با آن داشت، مانند تاس، می توانستند این بازی سه بعد را همان طور که در تصویر زیر نشان داده شده است، انجام دهند.
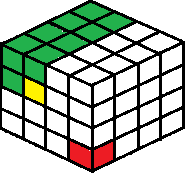
- در هنگام انجام یک حرکت، یکی مکعب انتخاب شده و همچنین هر مکعب به سمت چپ، بالا و بالای مکعب انتخاب شده را حذف می کرد. یک حرکت نمونه به رنگ زرد در تصویر برجسته شده است که تمام کاشی های سبز در تصویر را نیز حذف می کند. کسی که آخرین کاشی را می گیرد که توسط کاشی قرمز در تصویر نشان داده شده است، بازیکنی است که بازی را از دست می دهد.
- برای آسان تر کردن بازی با مکعب های واقعی، می توان مکعب ها را در برابر گوشه ای مانند گوشه یک جعبه کفش هل داد، به طوری که کاشی قرمز در گوشه بسیار جعبه قرار دارد، و تنها یک بار قابل دسترسی است که تمام مکعب های دیگر نیز حذف شده اند. با استفاده از یک جعبه لازم نیست، اما آن را مکعب تثبیت و آن را آسان تر به حذف مکعب بدون ضربه زدن به کل ساختار بیش از.

چه در مورد بازی Chomp در ابعاد حتی بیشتر؟
- پیش از این ما تعیین کرد که آن را به اندازه کافی آسان برای اضافه کردن یک بعد جدید به یک بازی Chomp. اگر کسی می خواست چامپ را در بعد حتی بالاتر از سه بعدی بازی کند، به اضافه کردن ابعاد جدید به تخته چامپ ادامه می داد. با این حال، پس از 3D هیچ راهی برای شبیه سازی یک تخته Chomp با استفاده از بلوک های دیگر وجود دارد. با این حال یک راه برای شبیه سازی بازی chomp با استفاده از مداد و کاغذ وجود دارد، و این روش به ما اجازه می دهد تا بازی را در هر تعداد از ابعاد، نه تنها 2D یا 3D.
- ما با بازی یک بازی Chomp 2D بر روی کاغذ شروع خواهد شد. روشی که می توان بازی را شبیه سازی کرد این است که ابتدا با انتخاب شماره ای که تنها ۲ عامل نخست مختلف دارد. به عنوان مثال، 72 = 2³ x 3². سپس تمام عوامل این عدد را به صورت مستطیل می نویسیم، همان طور که در زیر نشان داده شده است.
- 72 36 18 9
  24 12 6 3
  8 4 2 1
- هر عدد همسایه مناسب توسط یک عامل ۲ کوچکتر است و هر عدد همسایه در زیر توسط یک عامل ۳ کوچکتر است. برای انجام یک حرکت در این هیئت مدیره، یک عدد را انتخاب کنید. سپس آن عدد را به همراه هر یک از عوامل آن حذف می کردید. هر شماره ۷۲ را می گیرد بازی را از دست می دهد.
- برای داشتن مستطیل اولیه بزرگتر، می توان با استفاده از فرمول ۲^P x ۳ Q عدد بزرگتری پیدا^کرد. با جایگزینی P و Q با اعداد بزرگتر، یک تخته بزرگتر و بزرگتر برای Chomp دوD دریافت کنید.
- چگونه می توان این شبیه سازی را برای ابعاد بالاتر عمومی کرد؟
  - برای گسترش این مداد و نسخه کاغذی Chomp از 2D به 3D, یکی به سادگی نیاز به گسترش فرمول مورد استفاده برای پیدا کردن شماره شروع. به جای انتخاب عدد که تنها ۲ عامل نخست مختلف دارد، یک عدد را انتخاب می کرد که ۳ عامل نخست مختلف دارد. ما می توانیم از فرمول جدیدی برای پیدا کردن این عدد استفاده کنیم که به این قرار است: ۲^P x ۳^Q x ۵^R. سپس با استفاده از روش های مشابه قبل می توان بازی را در ۳ بعد شبیه سازی کرد. رفتن به ابعاد حتی بزرگتر به سادگی نیاز به اضافه کردن اعداد اول جدید به فرمول، بسته به تعداد ابعاد شما می خواهید.

مراجع