Chomp ©

វាល គឺជាចំណុចឆ្លងនៃជួរដេក និងជួរឈរ ដែលមានស្លាក (row, col)។
ក្បឿង គឺជារូបភាពនៅលើវាលមួយចំនួន។
ទីតាំង មានវាលទាំងអស់ដែលមានក្រឡា។

ចូរយើងចាប់ផ្តើមជាមួយនឹងបញ្ហាងាយៗ ពោលគឺមុខតំណែងតូច។ ដើម្បីបង្កើតពួកវាយើងចុច 'កុំព្យូទ័រ: បិទ' ។ ប្រសិនបើយើងចុចលើ (2,1) នៅសល់តែមួយជួរ។

តើកីឡាករបន្ទាប់អាចធ្វើអ្វីបាន ពោលគឺគូប្រកួតរបស់អ្នក?
- ដោយចុចលើ (1,2) នៅសល់តែក្រឡានៅលើ (1,1) ដូច្នេះអ្នកចាញ់។

អនុញ្ញាតឱ្យយើងចុច 'ហ្គេមថ្មី' ហើយនៅលើ (3,1) និង (2,2) ដើម្បីឱ្យមានក្រឡាមួយនៅជួរទី 2 និងទាំងអស់នៃជួរទី 1 ។

តើកីឡាករបន្ទាប់អាចធ្វើអ្វីបាន?
- ដោយចុចលើ (1,3) នៅសល់តែបីក្រឡាប៉ុណ្ណោះ។ ឃើញទេថាអ្នកគ្មានឱកាស?

តោះចុចលើ 'ហ្គេមថ្មី' ហើយចុចលើ (3,1) និង (2,3)។

តើកីឡាករបន្ទាប់អាចធ្វើអ្វីបាន?
- គូប្រជែងរបស់អ្នកអាចចុចលើ (1,4)។ ឃើញទេថាអ្នកគ្មានឱកាស?

តើអ្នកអាចសង្ខេបបានថាមុខតំណែងណាដែលមានក្រឡាត្រឹមតែ 2 ជួរដែលអ្នកគ្មានឱកាសឈ្នះហ្គេម?
- ប្រសិនបើជួរខាងលើមានក្រឡាមួយច្រើនជាងជួរទី 2 នោះមិនថាអ្នកធ្វើអ្វីក៏ដោយ គូប្រជែងរបស់អ្នកតែងតែអាចធ្វើចលនាបាន ដូច្នេះហើយជួរខាងលើមានក្រឡាមួយច្រើនជាងជួរទី 2 ។ បន្ទាប់មកមិនថាអ្នកធ្វើអ្វីទេ នៅទីបំផុតអ្នកនឹងត្រូវជ្រើសរើសក្បឿង (1,1) ហើយចាញ់ហ្គេម។

ប្រសិនបើក្រឡាក្បឿងត្រូវបានចុច ក្រឡាទាំងអស់ខាងក្រោម និងខាងស្តាំក៏ត្រូវដកចេញផងដែរ។ ច្បាប់នេះមាន ស៊ីមេទ្រី; ពោលគឺ ហ្គេមទាំងមូលមានស៊ីមេទ្រីដូចតទៅ៖ ប្រសិនបើយើងផ្លាស់ប្តូរជួរដេក និងជួរឈរ នោះច្បាប់នឹងនៅដដែល៖ ក្រឡាទាំងអស់ទៅខាងស្តាំក្លាយជាក្រឡាខាងក្រោមទាំងអស់ ហើយក្រឡាខាងក្រោមទាំងអស់ក្លាយជាក្រឡាទាំងអស់នៅខាងស្តាំនៃក្រឡាដែលបានដកចេញ។ ម្យ៉ាងវិញទៀត ប្រសិនបើយើងឆ្លុះមើលទីតាំងមួយនៅតាមបណ្តោយបន្ទាត់ដែលឆ្លងកាត់ (1,1) និង (2,2) នោះទីតាំងថ្មីអាចមើលទៅខុសគ្នា ប៉ុន្តែវាមានស្ថានភាពដូចគ្នា។ ចលនាដែលឈ្នះក៏នឹងក្លាយជាចលនាដូចគ្នាដែរ មានតែឆ្លុះបញ្ចាំងផងដែរ។

ទីតាំងដែលមានក្បឿងចំនួន 3 នៅជួរទីមួយ និងក្បឿង 2 នៅជួរទីពីរគឺគ្មានសង្ឃឹមដូចដែលយើងដឹងនោះទេ។ តើទីតាំងកញ្ចក់មានក្រឡាក្បឿងអ្វីខ្លះ?
- បន្ទាប់ពីឆ្លុះកញ្ចក់ វាមានក្រឡាចំនួន៣នៅជួរឈរខាងឆ្វេង និង២ក្បឿងនៅជួរទី២។

យើងដឹងថាមុខតំណែងអស់សង្ឃឹមទាំងអស់ដែលមានក្រឡាក្បឿងតែនៅក្នុងជួរពីរដំបូងប៉ុណ្ណោះ។ តើស៊ីមេទ្រីប្រាប់យើងអ្វីខ្លះអំពីទីតាំងអស់សង្ឃឹមដែលមានក្រឡាក្បឿងតែនៅក្នុងជួរឈរពីរដំបូង?
- ទីតាំងដែលគ្មានសង្ឃឹមជាមួយក្រឡាក្បឿងនៅក្នុងជួរឈរពីរដំបូងគឺជាកន្លែងដែលជួរឈរទីមួយមានក្បឿងមួយច្រើនជាងជួរឈរទីពីរ។

នេះគឺជាមុខតំណែងមួយទៀតដែលមិនមានឱកាស៖ ចុច 'ហ្គេមថ្មី' ហើយនៅលើ (4,1), (2,2) និង (1,4)។

ប្រសិនបើគូប្រជែងធ្វើចលនាក្នុងទីតាំងនេះ តើអ្នកឆ្លើយយ៉ាងណា?
- អ្នកត្រូវប្រាកដថា បន្ទាប់ពីអ្នកផ្លាស់ទីជួរខាងលើ ហើយជួរទីមួយមានប្រវែងដូចគ្នា។ តាមរយៈការធ្វើម្តងទៀតនូវគំរូនេះ គូប្រកួតនឹងត្រូវយកក្បឿង (1,1) ហើយចាញ់។

ដូច្នេះ ប្រសិនបើជួរទីមួយ និងជួរទីមួយមានចំនួនក្រឡាដូចគ្នា ហើយមិនមានក្បឿងផ្សេងទៀតទេ នោះទីតាំងនឹងអស់សង្ឃឹម។ តើមុខតំណែងណាខ្លះអាចផ្លាស់ប្តូរទៅជាមុខតំណែងបែបនេះ?
- ប្រសិនបើទីតាំងមួយមានចំនួនជួរដេក និងជួរឈរដូចគ្នា មិនថាមានក្រឡាប៉ុន្មានកន្លែងផ្សេងទៀតទេ៖ ការផ្លាស់ទីលើ (2,2) ទុកតែជួរទីមួយ និងជួរទីមួយដែលមានប្រវែងស្មើគ្នា ដោយទុកឱ្យគូប្រជែងគ្មានឱកាស។ ដូច្នេះប្រសិនបើទីតាំងមួយមានលេខដូចគ្នានៃក្រឡានៅក្នុងជួរខាងលើដូចនៅក្នុងជួរឈរខាងឆ្វេងនោះ អ្នកលេងនៅ (2,2) ហើយឈ្នះហ្គេម។

ដើម្បីលេង Chomp ឱ្យបានល្អ អ្នកត្រូវដឹងអំពីការឈ្នះ និងការបាត់បង់តំណែង។ ទីតាំងឈ្នះ គឺជាកន្លែងមួយដែលគេអាចពង្រឹងការឈ្នះ ប្រសិនបើគេលេងដោយសុទិដ្ឋិនិយម មិនថាភាគីម្ខាងទៀតធ្វើអ្វីនោះទេ។ បាត់បង់តំណែង គឺជាកន្លែងមួយដែលគ្មានឱកាស ប្រសិនបើភាគីម្ខាងទៀតលេងបានល្អ។ ចំណុចខាងក្រោមគឺជាអ្វីដែលមនុស្សម្នាក់ហៅថានិយមន័យក្នុងគណិតវិទ្យា។ នៅក្នុង Chomp មុខតំណែងចាញ់ និងឈ្នះត្រូវបានកំណត់តាមរយៈ 3 ចំណុចនេះ៖
1. ប្រសិនបើមានតែក្បឿងមួយនៅសល់ (នៅជ្រុងខាងឆ្វេងខាងលើ) នោះគឺជាទីតាំងបាត់បង់។
2. ទីតាំងមួយគឺជាទីតាំងឈ្នះប្រសិនបើមានមានចលនាដែលនាំឱ្យបាត់បង់តំណែងសម្រាប់គូប្រជែង។
3. ទីតាំងមួយគឺជាទីតាំងដែលបាត់បង់ ប្រសិនបើ រាល់ ការផ្លាស់ប្តូរលទ្ធផលនៅក្នុងទីតាំងឈ្នះសម្រាប់គូប្រជែង។
ប្រសិនបើក្រឡេកមើលដំបូង ចំណុចខាងលើអាចមើលទៅគ្មានប្រយោជន៍ ពីព្រោះមុខតំណែងឈ្នះត្រូវបានពន្យល់ដោយការបាត់បង់តំណែង ហើយការបាត់បង់តំណែងត្រូវបានពន្យល់ដោយមុខតំណែងឈ្នះ។ ទោះជាយ៉ាងណាក៏ដោយ និយមន័យគឺផ្អែកលើការផ្លាស់ទី ហើយគ្រប់លំដាប់នៃចលនានៅទីបំផុតនាំទៅដល់ទីតាំងក្បឿងតែមួយ ដែលយោងទៅតាមចំណុចទី 1 គឺជាទីតាំងបាត់បង់។

តើវាអាចទៅរួចទេដែលមានមុខតំណែងដែលភាគីទាំងសងខាងមិនអាចពង្រឹងការឈ្នះបាន? (ពិបាក)
- យើងនឹងបង្កើតទ្រឹស្តីបទតូចមួយ ហើយបញ្ជាក់វា។ ភស្តុតាងនឹងបង្ហាញយើងពីវិធីដើម្បីឈានដល់ភាពខ្លាំងនៃការលេងដ៏ល្អឥតខ្ចោះ។ ភ័ស្តុតាងគឺជាភ័ស្តុតាងមួយដោយការណែនាំដែលបង្ហាញថាសេចក្តីថ្លែងការណ៍ដែលយើងចង់បញ្ជាក់គឺពិតសម្រាប់ក្បឿងមួយហើយបន្ទាប់មកបង្ហាញថាប្រសិនបើវាជាការពិតសម្រាប់ចំនួន N នៃក្រឡា នោះវាក៏ត្រូវតែជាការពិតសម្រាប់ក្បឿងមួយបន្ថែមទៀត ពោលគឺ N +1 ក្បឿង។ ដោយសារសេចក្តីថ្លែងការណ៍នេះគឺពិតសម្រាប់ក្បឿង N=1 វាត្រូវតែពិតសម្រាប់ក្រឡា N+1=1+1=2។ ប៉ុន្តែជាការពិតសម្រាប់ N=2 នោះវាក៏ត្រូវតែពិតសម្រាប់ N+1=2+1=3 tiles ហើយដូច្នេះនៅលើ។ i.e. សម្រាប់ចំនួនក្បឿងណាមួយ។
- Lemma (ទ្រឹស្តីបទតូច)៖ ទីតាំងនីមួយៗគឺជាទីតាំងឈ្នះ ឬចាញ់។
- ភស្តុតាងដោយការណែនាំ៖
- មូលដ្ឋាន៖ ប្រសិនបើទីតាំងមានក្រឡាតែមួយ នោះក្បឿងនេះស្ថិតនៅជ្រុងខាងឆ្វេងខាងលើ ហើយបន្ទាប់មកទីតាំងគឺជាទីតាំងបាត់បង់ដោយយោងទៅតាមច្បាប់របស់ Chomp (បង្ហាញថា lemma គឺពិតប្រសិនបើមានតែ N =1 ក្បឿងមានវត្តមាន)។
- សម្មតិកម្មការបញ្ចូល៖ យើងសន្មត់ថា លេម៉ាគឺពិតសម្រាប់មុខតំណែង ទាំងអស់ ដែលមានរហូតដល់ទៅ N tiles ពោលគឺតំណែងដែលមាន 1,2,..., N ក្រឡាក្បឿង គឺឈ្នះឬចាញ់។ មុខតំណែង។
- ជំហានណែនាំ៖ ឥឡូវនេះ យើងចង់បង្ហាញថា តំណែងទាំងអស់ដែលមានក្រឡា N+1 ត្រូវតែជាតំណែងចាញ់ ឬឈ្នះ។
- នៅក្នុង P ខាងក្រោមគឺជាទីតាំងបំពានជាមួយនឹងក្រឡា N+1 ។ ប្រសិនបើ P ត្រូវបានកាត់បន្ថយដោយចលនាមួយ នោះមុខតំណែងថ្មីត្រូវតែមានក្រឡា ≤N ដូច្នេះវាជាការចាញ់ ឬជាទីតាំងឈ្នះ យោងទៅតាមសម្មតិកម្មចាប់ផ្តើម។ ប្រសិនបើ P អាចត្រូវបានកាត់បន្ថយក្នុងមួយចលនាទៅទីតាំងចាញ់នោះ P គឺជាទីតាំងឈ្នះ។ បើមិនដូច្នោះទេ P អាចត្រូវបានកាត់បន្ថយក្នុងមួយចលនាទៅទីតាំងឈ្នះ។ ប៉ុន្តែប្រសិនបើទីតាំងមួយអាចត្រូវបានកាត់បន្ថយក្នុងការផ្លាស់ទីទៅទីតាំងឈ្នះ នោះ P ត្រូវតែជាទីតាំងចាញ់។ នេះបង្ហាញថា P (មានក្រឡា N+1) គឺជាទីតាំងឈ្នះ ឬចាញ់។ នេះបង្ហាញថាមុខតំណែងទាំងអស់ (ជាមួយ N+2,N+3,... tiles) គឺជាតំណែងឈ្នះ ឬចាញ់។
  
  ចុងបញ្ចប់នៃភស្តុតាង ∎
- ការអត្ថាធិប្បាយបន្ថែម៖ ជំហានដំបូងផ្តល់នូវវិធីសាស្រ្តក្នុងការសម្រេចចិត្តសម្រាប់មុខតំណែងទាំងអស់ (រហូតដល់ទំហំខ្លះ) ថាតើពួកគេឈ្នះ ឬចាញ់តំណែង។ វាត្រូវបានកំណត់ដោយដូចខាងក្រោមៈ
  
  មួយចាប់ផ្តើមដោយ N=1 ហើយដាក់ស្លាកទីតាំងនោះថាជាទីតាំងបាត់បង់។ បន្ទាប់មកមួយកំណត់ស្ថានភាពនៃមុខតំណែងទាំងអស់ដោយ 2 ក្បឿង បន្ទាប់មកជាមួយនឹង 3 ក្បឿង និងបន្តបន្ទាប់គ្នា រាល់ពេលដែលប្រើប្រាស់ចំណេះដឹងអំពីស្ថានភាពនៃមុខតំណែងតូចជាង ហើយបន្ថែមទីតាំងបាត់បង់ដែលបានរកឃើញថ្មីទៅក្នុងបញ្ជីនៃមុខតំណែងបាត់បង់ដែលគេស្គាល់។
- នេះគឺជាវិធីដ៏មានប្រសិទ្ធភាពក្នុងការស្វែងរកមុខតំណែងឈ្នះ និងចាញ់ទាំងអស់រហូតដល់ទំហំមួយចំនួន។ នៅពេលដែលលេខកាន់តែធំ កម្មវិធីកុំព្យូទ័រនឹងមានប្រយោជន៍។ គ្រឿងផ្សំចាំបាច់មានដូចខាងក្រោម៖
  - នីតិវិធីដែលអាចបង្កើតទីតាំងទាំងអស់នៃក្បឿង N ប្រកបដោយប្រសិទ្ធភាពពីការដឹងពីទីតាំងទាំងអស់នៃក្រឡាក្បឿង N
  - នីតិវិធីដែលអាចពិនិត្យយ៉ាងមានប្រសិទ្ធភាពថាតើតំណែងមួយអាចត្រូវបានកាត់បន្ថយទៅតំណែងដែលបានផ្តល់ឱ្យផ្សេងទៀត។
  យើងនឹងទុកវាឱ្យអ្នកគិតបន្ថែមអំពីវា ហើយប្រហែលជាសរសេរកម្មវិធីកុំព្យូទ័របែបនេះ។

តើតំណែងចាញ់និងឈ្នះមានប៉ុន្មានគ្រាប់ពិតប្រាកដ?
- មានតែមុខតំណែងពីរប៉ុណ្ណោះដែលមានក្រឡាក្បឿង 2 យ៉ាងពិតប្រាកដ 2 ក្រឡានៅជួរខាងលើ ឬក្រឡាពីរនៅតាមបណ្តោយជួរឈរខាងឆ្វេង។ មុខតំណែងទាំងពីរនេះគឺជាតំណែងឈ្នះ។

តើតំណែងចាញ់និងឈ្នះប៉ុន្មានមាន៣គ្រាប់?
- មានមុខតំណែងសរុបចំនួន 3 ដែលមានក្រឡា 3 យ៉ាងពិតប្រាកដ។ ពួកគេមានទីតាំងឈ្នះ 2 និង 1 តំណែងចាញ់។ តើអ្នកអាចដឹងថាពួកគេជាមុខតំណែងមួយណាទេ?

តើតំណែងចាញ់និងឈ្នះប៉ុន្មានមានបួនគ្រាប់?
- មាន 5 មុខតំណែងដែលអាចមាន 4 យ៉ាងពិតប្រាកដ។ មុខតំណែងទាំងអស់នេះគឺជាតំណែងឈ្នះ។

តើមុខតំណែងចាញ់និងឈ្នះមានចំនួន៥គ្រាប់យ៉ាងប្រាកដ?
- មានមុខតំណែងសរុបចំនួន 7 ដែលមានចំនួន 5 យ៉ាងពិតប្រាកដ។ ពីមុខតំណែងទាំងនេះ 3 គឺចាញ់តំណែង និង 4 តំណែងឈ្នះ។ តើអ្នកអាចដឹងថាពួកគេជាមួយណា?

តើទីតាំងចតុកោណឈ្នះ ឬចាញ់តំណែង?
- លេម៉ាខាងក្រោមឆ្លើយសំណួរនេះ។ ភ័ស្តុតាងគឺជាភស្តុតាងនៃអត្ថិភាព។ វានឹងបង្ហាញតែពីអត្ថិភាពនៃការផ្លាស់ប្តូរដែលឈ្នះដោយមិនបង្ហាញពីអ្វីដែលជាការផ្លាស់ប្តូរនោះទេ។ យ៉ាងណាក៏ដោយ ការដឹងអំពីលេម៉ាគឺមានប្រយោជន៍សម្រាប់ការលេងរបស់អ្នកដូចបានពន្យល់ខាងក្រោម។
- ឡែមម៉ា៖ ទីតាំងចតុកោណទាំងអស់ លើកលែងតែទីតាំង 1-tile គឺជាមុខតំណែងឈ្នះ។
- ភស្តុតាង៖ ដើម្បីបង្ហាញថានេះជាការពិត យើងត្រូវពិចារណាករណីពីរដែលអាចកើតមាន៖
  1. ការដកក្បឿងនៅជ្រុងខាងស្តាំនៃក្តារគឺជាចលនាឈ្នះៗ។
  2. ការដកក្បឿងនៅជ្រុងខាងស្តាំក្រោមមិនមែនជាចលនាឈ្នះៗទេ។
- ប្រសិនបើករណីទី 1 ជាការពិត នោះមានន័យថា ចតុកោណកែងគឺជាទីតាំងឈ្នះ ហើយនេះគាំទ្រឡឹមម៉ា។
- ប្រសិនបើករណីទី 1 មិនពិត នោះយើងត្រូវពិចារណាករណីទី 2។ យោងតាមភ័ស្តុតាងដែលយើងបានធ្វើពីមុន ទីតាំងដែលកើតចេញពីការដកក្បឿងនៅជ្រុងខាងស្តាំខាងក្រោមត្រូវតែជាទីតាំងឈ្នះ ដែលមានន័យថាវាត្រូវតែមានចលនាឈ្នះ ដែលមាន។ ប៉ុន្តែ ដោយសារចលនានីមួយៗក្នុងចតុកោណកែងដកក្បឿងនៅជ្រុងខាងស្តាំខាងក្រោម ទីតាំងចាញ់ដែលកើតចេញពីចលនាទី 2 (ចលនាឈ្នះ) គឺដូចគ្នាថាតើចលនាឈ្នះត្រូវបានលេងបន្ទាប់ពីការផ្លាស់ទីជ្រុង ឬជំនួសឱ្យការផ្លាស់ទីជ្រុង។ នេះមានន័យថាចលនាឈ្នះអាចត្រូវបានគេលេងភ្លាមៗ ដូច្នេះបង្ហាញថាចលនាឈ្នះមានសម្រាប់ទីតាំងចតុកោណ។
- ចុងបញ្ចប់នៃភស្តុតាង ∎
- មតិបន្ថែម៖ ថ្វីត្បិតតែលេម៉ាមិនប្រាប់យើងពីអ្វីដែលចលនាឈ្នះគឺវាមានប្រយោជន៍ក្នុងការដឹងថាទីតាំងចតុកោណគឺជាមុខតំណែងឈ្នះ។ ដូច្នេះមិនគួរធ្វើចលនាដែលបង្កើតទីតាំងចតុកោណទេ (លើកលែងតែទីតាំង 1x1)។

តើអ្នកអាចកំណត់សម្រាប់ក្ដារការ៉េណាមួយថាតើការផ្លាស់ទីឈ្នះគឺជាអ្វី?
- សម្រាប់ការ៉េទាំងអស់នៃទំហំ>1 ចលនាឈ្នះតែមួយគត់គឺនៅលើ (2,2)។

សម្រាប់មុខតំណែងណាដែលស្រដៀងនឹងការ៉េគឺជាចលនាដូចគ្នាជាចលនាឈ្នះ?
- ការផ្លាស់ប្តូរ (2,2) ក៏ជាចលនាឈ្នះៗសម្រាប់ទីតាំងណាមួយដែលជួរទី 1 និងជួរទី 1 មានប្រវែងដូចគ្នា។

តើទីតាំងមួយអាចមានចលនាឈ្នះច្រើនជាងមួយបានទេ?
- បាទ / ចាស ទីតាំងមួយអាចមានច្រើនជាងចលនាឈ្នះមួយ។ ពិចារណាលើមុខតំណែងខាងក្រោម៖
  
  ###
  ##
  #
  
  ទីតាំងក្រុមប្រឹក្សាភិបាលនេះមានចលនាឈ្នះ 3 ផ្សេងគ្នាដែលអាចធ្វើបាន។ តើអ្នកអាចកំណត់ថាពួកគេជាអ្វី?

យុទ្ធសាស្ត្រទូទៅសម្រាប់ការឈ្នះនៅ Chomp គឺបង្កើតទីតាំងចាញ់សម្រាប់គូប្រជែងរបស់អ្នក ដើម្បីកុំឱ្យពួកគេមានឱកាស។ យើងក៏ចង់ជៀសវាងការបង្កើតមុខតំណែងឈ្នះដែលគូប្រជែងអាចប្រែក្លាយទៅជាការបាត់បង់តំណែងសម្រាប់យើង។

គន្លឹះក្នុងការឈ្នះគឺត្រូវដឹងពីមុខតំណែងចាញ់ឱ្យបានច្រើនតាមដែលអាចធ្វើទៅបាន និងស្វែងយល់ពីរបៀបបង្កើតមួយមុនពេលគូប្រជែងរបស់អ្នកធ្វើ។ ចូរយើងពិចារណាលើក្រុមប្រឹក្សាភិបាលដែលអាចមានដូចខាងក្រោម ដែលជាទីតាំងបាត់បង់ដែលគេស្គាល់៖

#######
###
###
#
#
រូបភាពទី 1

តើមុខតំណែងអ្វីខ្លះដែលអាចប្រែក្លាយទៅជាមុខតំណែងដែលបាត់បង់នេះក្នុងចលនាមួយ?

ទីតាំង ចាញ់ ខាង លើ អាច ជា លទ្ធផល ពី ការ ផ្លាស់ទី ណា មួយ ដែល មាន សញ្ញា + ខាង ក្រោម ៖

#######+
###
###
#
#

#######
###+
###
#
#

#######
###
###
#+
#

#######
###
###
#
#
+

រូបភាពទី២

ការ ផ្លាស់ទី ទាំង នេះ គឺ ស្ថិត នៅ ក្នុង ជ្រុង កាត់ ។ តើ ការ ផ្លាស់ទី + បែប នេះ នឹង កាត់ ក្រឡា ដែល អាច លេច ឡើង នៅ ក្នុង រូបភាព ខាង ក្រោម ជាមួយ ដែរ ឬ ទេ ?:

#######+?
###
###
#
#

#######
###+???
###????
#
#

#######
###
###
#+?
#??

#######
###
###
#
#
+
?

រូបភាព ៣

ក្រឡា + ក្រឡា គឺ ចាំបាច់ ហើយ ? ក្រឡា គឺ ជា ជម្រើស &; # 160; ។ នៅ ក្នុង ទី តាំង ឈ្នះ ខាង ឆ្វេង ជួរ កំពូល អាច ត្រូវ បាន ពង្រីក ដោយ អចេតនា ទៅ ខាង ស្តាំ ជាមួយ នឹង ' ? ' ហើយ នៅ ក្នុង ទី តាំង ឈ្នះ ត្រឹម ត្រូវ ជួរ ឈរ ទី មួយ អាច ត្រូវ បាន ពង្រីក ដោយ អចេតនា ទៅ បាត ជាមួយ នឹង ' ? ' បន្ថែម ទៀត ។ តំណែង ទាំង អស់ នេះ ក៏ កំពុង ឈ្នះ តំណែង ផង ដែរ ។ បើយើងត្រូវធ្វើចលនាក្នុងឋានៈបែបនេះ យើងនឹងយក ក្រណាត់ + ក្រឡា ដូច្នេះទាំងអស់គ្នា ? ក្រឡា ដែល ត ភ្ជាប់ ក៏ នឹង ត្រូវ បាន ដក ចេញ ផង ដែរ ដែល នាំ ឲ្យ មាន ទី តាំង ចាញ់ ដែល យើង បាន ចាប់ ផ្តើម ។

តើ មាន ការ ឈ្នះ ឬ ចាញ់ តំណែង ច្រើន ជាង នេះ ឬ ទេ ?
- សម្រាប់ តំណែង ចាញ់ នីមួយ ៗ មាន មុខ តំណែង ជា ច្រើន ដែល អាច ក្លាយ ទៅ ជា តំណែង ចាញ់ នេះ ដោយ ការ ផ្លាស់ ប្តូរ តែ មួយ ។ ដូច្នេះ តំណែង ទាំង អស់ នេះ គឺ ជា តំណែង ឈ្នះ ។
- ដូច្នេះ មាន តំណែង ឈ្នះ ច្រើន ជាង ការ ចាញ់ តំណែង ។ ដូច្នេះ វា មាន ប្រសិទ្ធភាព បំផុត ក្នុង ការ ចងចាំ ពី ការ ចាញ់ តំណែង ឲ្យ បាន ច្រើន តាម ដែល អាច ធ្វើ ទៅ បាន តំណែង ផ្សេង ទៀត ទាំង អស់ គឺ ឈ្នះ តំណែង ។

ធ្វើ បញ្ជី នៃ ការ បាត់ បង់ តំណែង ដែល អ្នក ដឹង ហើយ សម្រាប់ ទីតាំង នីមួយៗ សរសេរ ទីតាំង ឈ្នះ ទាំង អស់ ដែល ត្រូវ គ្នា និង របៀប រក ឃើញ ពួក គេ

ឧទាហរណ៍ ខាង ក្រោម នេះ បង្ហាញ ពី អត្ថន័យ របស់ យើង ៖

ដូច ដែល បាន បង្ហាញ ពី មុន នៅ ពេល ដែល តំណែង នេះ មាន តែ ២ ជួរ ប៉ុណ្ណោះ ហើយ ជួរ កំពូល មាន ក្រឡា មួយ ក្រឡា ច្រើន ជាង ជួរ ទី ពីរ ជាង នេះ គឺ ជា ទីតាំង ចាញ់ ដូច ដែល បាន បង្ហាញ ខាង ក្រោម៖

#####
####
ការ យក តំណែង ចាញ់ ដែល គេ ស្គាល់ នេះ យើង អាច កំណត់ ថា តំណែង ឈ្នះ ស្រប គ្នា គឺ ៖

#####+?
####

#####
####+

#####
####
+???
????

នៅ ទីតាំង ខាង ឆ្វេង អាច មាន ចំនួន ឬទេ ? ចំពោះសិទ្ធិនៃជួរឈរកំពូល ហើយនៅក្នុងទីតាំងត្រឹមត្រូវអាចមានជួរដេកច្រើន ? នៅក្រោម។ យើង អាច សង្ខេប ពាក្យ ពី របៀប រក ឃើញ តំណែង ឈ្នះ ទាំង នេះ (ដែល អ្នក គួរ ចងចាំ សម្រាប់ ការ លេង របស់ អ្នក) ៖

- តំណែង ជា ទីតាំង ឈ្នះ ដែល កាត់ បន្ថយ
  #####
  ####
- - បើ មាន តំណែង ណា មួយ មាន តែ ពីរ ជួរ ប៉ុណ្ណោះ ហើយ ជួរ ទី ១ មិន មែន ជា ក្រឡា មួយ ក្រឡា យូរ នោះ ជួរ ទី ពីរ ឬ
- - បើ តំណែង នេះ មាន ច្រើន ជាង ពីរ ជួរ ហើយ ជួរ ទី ១ គឺ ក្រឡា មួយ ក្រឡា យូរ ជាង នោះ ជួរ ទី ២ ។
ប៉ុន្តែ ក៏ មាន អ្វី ជា ច្រើន ទៀត ដែល ត្រូវ គិត ផង ដែរ ។ យើង មិន ត្រឹម តែ ចង់ លេង ត្រឹម ត្រូវ នៅ ក្នុង តំណែង ឈ្នះ បែប នេះ ប៉ុណ្ណោះ ទេ យើង ក៏ ចង់ ជៀស វាង ការ ផ្លាស់ ប្តូរ មួយ ដែល បង្កើត តំណែង ឈ្នះ បែប នេះ ផង ដែរ ។ នេះ មាន ន័យ ថា យើង មិន គួរ ធ្វើ ការ ផ្លាស់ ប្តូរ ដែល មាន តែ ពីរ ជួរ ប៉ុណ្ណោះ ដែល នៅ សល់ ឬ ជួរ ទី ពីរ មាន ក្រឡា មួយ តិច ជាង បន្ទាប់ មក ជួរ ទី មួយ ។

ដើម្បី សង្ខេប យើង ចង់ បង្កើត តំណែង ដែល បាត់ បង់ ប៉ុន្តែ យើង ក៏ ចង់ ជៀស វាង ពី ការ បង្កើត តំណែង ដែល ជា ការ ផ្លាស់ ប្តូរ មួយ ពី តំណែង ដែល បាត់ បង់ ។

រឿង មួយ ទៀត ដែល ត្រូវ កត់ សម្គាល់ ៖ ដោយសារ តែ រមណីមាត្រ កញ្ចក់ ដែល បាន លើក ឡើង កាល ពី មុន មតិ យោបល់ ខាង លើ ទាំង អស់ អាច ត្រូវ បាន ធ្វើ ឡើង វិញ ដោយ គ្រាន់ តែ ជំនួស ពាក្យ "ជួរ" ដោយ ពាក្យ "column"។

វា ត្រូវ បាន ទុក ឲ្យ អ្នក ប្រមូល តំណែង ដែល បាត់ បង់ បន្ថែម ទៀត និង មុខ តំណែង ឈ្នះ ដូច គ្នា របស់ ពួក គេ ដែល ជា ការ ផ្លាស់ ប្តូរ មួយ ។

ចុះ បើ អ្នក ត្រូវ លេង នៅ ក្នុង ទីតាំង ចាញ់ ?
- ប្រសិន បើ អ្នក ដឹង ថា អ្នក ត្រូវ តែ ធ្វើ ការ ផ្លាស់ទី ក្នុង ទីតាំង ចាញ់ នោះ តាម ទ្រឹស្តី អ្នក គ្មាន ឱកាស អ្វី ឡើយ ។ អ្វី ដែល អ្នក អាច ធ្វើ បាន គឺ សង្ឃឹម ថា គូ ប្រកួត របស់ អ្នក មិន ដឹង ពី ការ ផ្លាស់ ប្តូរ ជ័យ ជម្នះ ទាំង អស់ សម្រាប់ តំណែង ដែល អ្នក អាច បង្កើត ជាមួយ នឹង ការ ផ្លាស់ទី បន្ទាប់ របស់ អ្នក ទេ ។ អ្វី ដែល អ្នក អាច ធ្វើ បាន គឺ យក តែ ក្រឡា តែ មួយ ចេញ ពី ជ្រុង ប៉ុណ្ណោះ ។ នេះ ផ្តល់ ឲ្យ គូ ប្រកួត របស់ អ្នក នូវ ទីតាំង ដែល មាន ទំហំ អតិបរមា ហើយ វា ធ្វើ ឲ្យ គូ ប្រកួត របស់ អ្នក កាន់ តែ ពិបាក ក្នុង ការ ដឹង ពី ការ ផ្លាស់ទី ឈ្នះ ដូច គ្នា ។

តើ ត្រូវ រៀន ពី ការ បាត់បង់ តំណែង ដោយ ខ្លួន ឯង យ៉ាង ដូចម្ដេច ?
- មនុស្ស ម្នាក់ នឹង ត្រូវ អនុវត្ត នូវ អ្វី ដែល គេ ស្គាល់ ថា ជា ការ ស្វែង រក ដើម ឈើ ទាំង ស្រុង ។ អ្នក លេង ទី មួយ ចាប់ ផ្តើម ដោយ ទាយ ការ ផ្លាស់ទី បន្ទាប់ មក អ្នក លេង ទី ពីរ ទាយ ពី ការ ផ្លាស់ទី ហើយ ដូច្នេះ រហូត ដល់ អ្នក លេង ម្នាក់ និយាយ ថា អ្នក លេង A ឈ្នះ ។ បន្ទាប់ មក កីឡា ករ B ត្រូវ បាន អនុញ្ញាត ឲ្យ ផ្លាស់ ប្តូរ ការ ផ្លាស់ ប្តូរ ចុង ក្រោយ ដែល ពួក គេ បាន ធ្វើ ហើយ វា គឺ ជា វេន របស់ អ្នក លេង A បន្ទាប់ ទៀត ។ ប្រសិន បើ នៅ ក្នុង ទី តាំង មួយ កីឡា ករ ដែល លេង បន្ទាប់ B រត់ ចេញ ពី ការ ផ្លាស់ ប្តូរ ពីព្រោះ ការ ផ្លាស់ ប្តូរ ទាំង អស់ នាំ ឲ្យ មាន ការ ចាញ់ នោះ នេះ គឺ ជា ទី តាំង ចាញ់ ហើយ កីឡា ករ B អាច ផ្លាស់ ប្តូរ ការ ផ្លាស់ ប្តូរ ចុង ក្រោយ ដែល បាន ធ្វើ មុន ពេល ការ ចាញ់ ទី តាំង នេះ ត្រូវ បាន សម្រេច ។
- ' ការ ស្វែង រក ដើម ឈើ ' នេះ បន្ត រហូត ដល់ វា ច្បាស់ ថា តើ ទី តាំង ចាប់ ផ្តើម គឺ ជា ទី តាំង ចាញ់ ឬ ក៏ ការ ផ្លាស់ ប្តូរ របស់ កីឡា ករ 1 ប្តូរ វា ទៅ ជា ទី តាំង ចាញ់ ។
- នេះ អាច ជា ដំណើរ ការ ដ៏ វែង មួយ ប្រសិន បើ មនុស្ស ម្នាក់ ព្យាយាម ធ្វើ វា នៅ លើ ក្ដារ ដំបូង ដែល មាន ក្រឡា ជា ច្រើន ។ ទោះ ជា យ៉ាង ណា ក៏ ដោយ ការ បាត់ បង់ តំណែង កាន់ តែ ច្រើន យើង ដឹង ថា លំដាប់ នៃ ការ ផ្លាស់ ប្តូរ គឺ ខ្លី ជាង មុន ពេល ទី តាំង បែប នេះ ត្រូវ បាន សម្រេច ដូច្នេះ ការ ស្វែង រក ទាំង មូល គឺ លឿន ជាង មុន ។ ប្រសិន បើ យើង បាន ដឹង ថា អ្វី ៗ ទាំង អស់ មាន ការ បាត់ បង់ តំណែង នោះ តំណែង ចាប់ ផ្តើម នឹង ត្រូវ បាន ទទួល ស្គាល់ ថា ជា ទី តាំង ចាញ់ ឬ មាន តែ ការ ផ្លាស់ ប្តូរ មួយ ប៉ុណ្ណោះ ដែល ចាំបាច់ ដើម្បី កាត់ បន្ថយ វា ទៅ ជា ទី តាំង ចាញ់ ។

តើធ្វើដូចម្តេចដើម្បីរៀនបាត់បង់មុខតំណែងជាមួយកុំព្យូទ័រ?
- នៅ ក្នុង កម្រិត ពិបាក 'Very Hard' និង មុខ តំណែង មិន ធំ ជាង 8 x 15 កុំព្យូទ័រ លេង យ៉ាង ល្អ ឥត ខ្ចោះ ដូច្នេះ ទីតាំង នីមួយៗ ដែល ទទួល បាន លទ្ធផល ពី ការ ផ្លាស់ ប្តូរ កុំព្យូទ័រ គឺ ជា ការ បាត់ បង់ ការ បង្ហោះ ! មនុស្ស ម្នាក់ គួរ តែ ចាប់ ផ្តើម ជាមួយ ក្តារ តូច ៗ និង លេង ប្រឆាំង នឹង កុំព្យូទ័រ នៅ ក្នុង កម្រិត ' ពិបាក ខ្លាំង ណាស់ ' និង រៀន ពី មុខ តំណែង ទាំង អស់ ដែល កុំព្យូទ័រ បង្កើត ។ សម្រាប់ ទីតាំង នីមួយៗ បែប នេះ សូម គិត ពី របៀប ដែល ការ ផ្លាស់ទី នីមួយៗ របស់ អ្នក នឹង ត្រូវ បាន ឆ្លើយ ដោយ កុំព្យូទ័រ ដែល ប្តូរ វា ម្តង ទៀត ទៅ ជា ទីតាំង ដែល បាត់បង់ តូច ជាង នេះ ។ សម្រាប់ ទីតាំង ចាញ់ នីមួយៗ ក៏ ជា ទីតាំង កញ្ចក់ (ជួរឈរ <--> ជួរ ឈរ) គឺ ជា ទីតាំង ចាញ់ មួយ។
- តើអ្វីទៅជាចលនាដំបូងដែលគួរឲ្យសុទិដ្ឋិនិយម?
  - នៅ ក្នុង ការ ប្រកួត ទីតាំង ចាប់ ផ្តើម នឹង ក្លាយ ជា ចតុកោណ នៃ ដំបង ។ តាម ការ បញ្ជាក់ ពី មុន ចតុកោណ ជា ទីតាំង ឈ្នះ ប៉ុន្តែ តើ ការ ផ្លាស់ទី ដំបូង ផ្លាស់ ប្តូរ វា ទៅ ជា ទីតាំង ចាញ់ សម្រាប់ គូ ប្រកួត ? យើង បាន រៀន ពី មុន ថា ការ ផ្លាស់ទី ដ៏ ប្រសើរ បំផុត សម្រាប់ ការ៉េ គឺ ជា ក្រឡា ( 2,2 ) ប៉ុន្តែ ចុះ បើ ចតុកោណ មិន មែន ជា ការ៉េ ?
  - គ្រាន់ តែ ផ្លាស់ ប្តូរ ទៅ កម្រិត ពិបាក ' ខ្លាំង ណាស់ ' ហើយ អនុញ្ញាត ឲ្យ កុំព្យូទ័រ ធ្វើ ការ ផ្លាស់ ប្តូរ ដំបូង ។ ដរាប ណា ចតុកោណ មិន ធំ ជាង 8x15 កុំព្យូទ័រ លេង បាន ល្អ បំផុត ហើយ នឹង បង្ហាញ ពី ការ ផ្លាស់ទី ដំបូង ដ៏ ល្អ ឥត ខ្ចោះ ។ សាកល្បង ទំហំ ចតុកោណ ខុសៗ គ្នា ហើយ ចងចាំ ពី ការ ផ្លាស់ទី ដំបូង ដ៏ ប្រសើរ បំផុត ព្រោះ ការ ចាក់ កុំព្យូទ័រ នឹង មិន អាច ប្រើ បាន នៅ ថ្ងៃ ប្រកួត :)។
- មិន យូរ ប៉ុន្មាន អ្នក នឹង មិន អាច ទ្រាំ បាន ក្នុង កម្រិត លំបាក ងាយ ស្រួល និង មធ្យម ។

តើ មាន គ្រួសារ មិន កំណត់ ក្នុង ការ បាត់ បង់ តំណែង ឬ ទេ ?
- យើង បាន ជួប ក្រុម គ្រួសារ ទាំង ពីរ នេះ រួច ទៅ ហើយ ក្នុង ការ បាត់ បង់ តំណែង ។ N គឺ ជា អ្នក នាំ ពាក្យ វិជ្ជមាន ណា មួយ ។
- នេះ គឺ ច្រើន ជាង នេះ ៖

អ្នក លេង កុំព្យូទ័រ ដែល បាន ស្ថាបនា ឡើង ក្នុង ល្បែង ប្រើ បច្ចេកទេស ផ្សេង គ្នា សម្រាប់ កម្រិត លេង ផ្សេង គ្នា & # 160; ។

- ងាយស្រួល - ធ្វើ ការ ផ្លាស់ទី ដោយ ចៃដន្យ នីមួយៗ & # 160; ។ ប្រសិន បើ រក ឃើញ ទីតាំង ឈ្នះ ដ៏ សាមញ្ញ មួយ វា នឹង ផ្លាស់ទី ទៅ ទី នោះ ។
- មធ្យម - នៅ តែ ផ្លាស់ ប្តូរ ដោយ ចៃដន្យ ប៉ុន្តែ មាន ចំណេះ ដឹង កាន់ តែ ច្រើន អំពី ការ ឈ្នះ និង ចាញ់ តំណែង ។ នឹង ជៀស វាង ការ ផ្លាស់ ប្តូរ ដែល ផ្តល់ ឲ្យ គូ ប្រកួត ចូល ទៅ ក្នុង ការ ផ្លាស់ ប្តូរ ដ៏ សាមញ្ញ មួយ ដែល ឈ្នះ ។
- ពិបាក - មាន ចំណេះ ដឹង កាន់ តែ ច្រើន អំពី ការ ឈ្នះ តំណែង ។ ស្វែង រក យ៉ាង សកម្ម នូវ ក្រុម ប្រឹក្សាភិបាល សម្រាប់ ការ ផ្លាស់ ប្តូរ ដែល អាច បង្ខំ គូ ប្រកួត ឲ្យ ធ្វើ ការ ចាញ់ ផ្លាស់ ប្តូរ ដោយ ខ្លួន ឯង ។
- ពិបាកណាស់ - នឹង តែង តែ ធ្វើ ការ ផ្លាស់ទី ដ៏ ប្រសើរ បំផុត សម្រាប់ ទីតាំង ណា មួយ ដែល សម ទៅ នឹង ចតុកោណ ទំហំ 8x15 ។
កម្រិត ពិបាក កាន់ តែ ខ្ពស់ វា នឹង ពិបាក ជាង នេះ គឺ បង្ខំ កុំព្យូទ័រ ឲ្យ បាត់ បង់ ទីតាំង ។ កម្រិត នីមួយៗ ដឹង ថា មាន អ្នក ឈ្នះ និង ចាញ់ តំណែង ច្រើន ជាង កម្រិត មុន ហើយ ពិបាក ជាង នេះ ទៅ ទៀត ការ លំបាក កាន់ តែ ខ្លាំង ការ ឈ្នះ និង ចាញ់ តំណែង អ្នក នឹង ត្រូវ ដឹង ដើម្បី ព្យាយាម បង្ខំ កុំព្យូទ័រ ឲ្យ បាត់ បង់ ទីតាំង ។

មតិ យោបល់ ខាង ក្រោម នេះ នឹង មិន ជួយ ឲ្យ កាន់ តែ ខ្លាំង ឡើង នៅ ក្នុង Chomp នោះ ទេ ប៉ុន្តែ ពួកគេ នឹង ផ្តល់ នូវ ការ ពិត ដែល គួរ ឲ្យ ចាប់ អារម្មណ៍ មួយ ចំនួន និង ផ្តល់ ឱកាស មួយ ទៀត ដល់ យើង ក្នុង ការ អនុវត្ត ភស្តុតាង ដោយ ការ ជំរុញ។

តើ មាន មុខ តំណែង ខុស គ្នា ប៉ុន្មាន ដែល រួម មាន ក្ដារ ទទេ សម ទៅ នឹង ចតុកោណ ដែល មាន ជួរ ឈរ P rows និង Q?
- ប្រសិនបើយើងបញ្ចូលចតុកោណទទេយើងអាចគណនាចំនួនសរុបនៃមុខតំណែងដែលអាចប្រើប្រាស់រូបមន្តដូចខាងក្រោម៖ \[\frac{(P+Q)!}{P!Q!}\]តើ អ្នក អាច គណនា លេខ នោះ សម្រាប់ P និង Q តូច មួយ ហើយ ផ្ទៀង ផ្ទាត់ ថា វា ត្រឹមត្រូវ ឬ ទេ ?
- ១. ដើមកំណើតដំបូងនៃរូបមន្តកែច្នៃឡើងវិញ
  - Let f(P,Q) ជាចំនួននៃមុខតំណែងនៅក្នុងចតុកោណទំហំ PxQ។ ការ សង្កេត ដ៏ សំខាន់ មួយ គឺ ថា គ្រប់ មុខ តំណែង មាន រូបរាង នៃ ជណ្តើរ ដែល ជួរ នីមួយ ៗ មាន ក្រឡា ច្រើន ដូច ជួរ ខាង លើ ប៉ុន្តែ មិន ច្រើន ជាង នេះ ទេ ។
  - សូម ចាប់ ផ្ដើម ដំបូង ដោយ ប្រើ វិធី មួយ ដែល យើង អាច តំណាង ឲ្យ ជណ្តើរ ទាំង អស់ នេះ ។ វិធី មួយ ដើម្បី បង្កើត ជណ្តើរ យ៉ាង ងាយ ស្រួល គឺ ត្រូវ ចាប់ ផ្តើម នៅ ជ្រុង ខាង ឆ្វេង ខាង ក្រោម នៃ ក្តារ ហើយ ផ្លាស់ ទី ទៅ ខាង ស្តាំ ឬ ឡើង ។ មនុស្ស ម្នាក់ អាច បន្ត ធ្វើ ការ ផ្លាស់ទី ទាំង នេះ បាន រហូត ដល់ ពួក គេ ទៅ ដល់ ជ្រុង ខាង ស្តាំ កំពូល នៃ ក្ដារខៀន ។ យើង នឹង ហៅ រឿង នេះ ថា ជា ផ្លូវ មួយ ដែល យើង បាន យក មក ពី ( P,0 ) ទៅ ( 0,Q ) ។
  - ចំនួន មុខតំណែង គឺ ដូចគ្នា នឹង ចំនួន ផ្លូវ ពី (P,0) ទៅ (0,Q) ដរាប ណា មួយ ត្រូវ បាន អនុញ្ញាត ឲ្យ ឡើង ឬ ទៅ ខាង ស្ដាំ តែ ប៉ុណ្ណោះ។ លេខ f(P,Q+1) នៃ ផ្លូវ ដើម្បី ទទួល បាន ពី (P,0) ទៅ (0,Q+1) ជា លេខ f(P,Q) នៃ ផ្លូវ ដើម្បី ទទួល បាន ពី (P,0) ទៅ (0,Q), បន្ទាប់មកទៅ (0,Q+1) + លេខ f(P-1,Q) នៃផ្លូវដើម្បីទទួលបានពី (P,0) ទៅ (1,Q) បន្ទាប់មកទៅ (1, Q) បន្ទាប់មកទៅ (1, Q+1) និង (0,Q+1) ជាដើម។ រូបមន្តដែលឆ្លើយឆ្លងគ្នាមានដូចខាងក្រោម៖\[f(P,Q+1) = f(P,Q) + f(P-1,Q) + f(P-2,Q) + \ldots + f(1,Q) + f(0,Q)\]
  - ឥឡូវ នេះ យើង នឹង យក រូបមន្ត នេះ ហើយ ជំនួស P ដោយ P + 1 ។ បើ យើង ដោត P + 1 ទៅ ក្នុង រូបមន្ត ជំនួស P យើង ទទួល បាន ដូច ខាង ក្រោម៖ \[f(P+1,Q+1) = f(P+1,Q) + f(P,Q) + f(P-1,Q) + \ldots + f(0,Q)\] \[f(P+1,Q+1) = f(P+1,Q) + f(P,Q+1)\]ពី derivation ថ្មី នេះ យើង អាច កំណត់ រូបមន្ត \(f(P,Q) = f(P,Q-1) + f(P-1,Q)\) កន្លែងណា \(f(P,0) = 1\) និង \(f(0,Q) = 1\).
- ទំរង់ជំនួសនៃរូបមន្តប្តូរទិស
  - ជា ញឹកញាប់ មាន វិធី ជា ច្រើន ដើម្បី រាប់ ក្នុង បញ្ហា រួម គ្នា ។ ខាងក្រោមនេះ នឹងផ្តល់នូវវិធីដ៏ប្លែក និងប្រណិតជាងមុន ដើម្បីយករូបមន្តនេះមកធ្វើជាប្រភព។
  - យើង នឹង ប្រើ តំណាង ដូច គ្នា ដែល យើង បាន ប្រើ ពី មុន ជា កន្លែង ដែល យើង ចង់ ស្វែង រក ចំនួន សរុប នៃ ផ្លូវ ដែល នាំ យើង ពី ( P,0 ) ទៅ ( 0,Q ) ។ យើង អាច រៀបចំ ផ្លូវ ទាំង នេះ ទៅ ជា ពីរ ក្រុម ។
  - ផ្លូវ ដែល ចាប់ ផ្តើម ដោយ ការ ផ្លាស់ទី ដំបូង ទៅ ខាង ស្តាំ ពី (P,0) ទៅ (P,1)។ យើងដឹងហើយថា នៅក្នុងក្រុមនេះ យើងនឹងមានផ្លូវ f(P,Q-1) សរុបពី (P,1) ទៅ (0,Q)។ យើង ដឹង រឿង នេះ ពីព្រោះ ចតុកោណ ដែល នៅ សល់ បន្ទាប់ ពី ផ្លាស់ទី មួយ ទៅ ខាង ស្តាំ គឺ ទំហំ P x (Q-1)។
  - ក្រុម ផ្សេង ទៀត គឺ ជា ផ្លូវ ដែល ចាប់ ផ្តើម ដោយ ការ ផ្លាស់ ប្តូរ ដំបូង ដែល ធ្វើ ដំណើរ មួយ ផ្លាស់ ទី ពី ( P,0 ) ទៅ ( P-1,0 ) ។ នៅក្នុងក្រុមនេះ យើងដឹងថាមាន f(P-1,Q) លើផ្លូវសរុប ដោយហេតុថា ចតុកោណដែលបណ្តាលមកពីទំហំ (P-1) x Q។
  - ដូច្នេះ ដោយ សារ គ្រប់ ផ្លូវ ដែល អាច ធ្វើ ទៅ បាន នឹង ធ្លាក់ ទៅ ក្នុង ក្រុម មួយ ក្នុង ចំណោម ក្រុម ទាំង ពីរ នេះ ចំនួន សរុប នៃ ផ្លូវ គឺ ចំនួន សរុប នៃ ក្រុម ទាំង នេះ ។ នេះ ផ្ដល់ ឲ្យ យើង នូវ រូបមន្ត ដូចគ្នា \(f(P,Q) = f(P,Q-1) + f(P-1,Q)\).
- ៤. ដើមកំណើតនៃរូបមន្តច្បាស់លាស់
  - ជំនួស ឲ្យ ការ ចាប់ ផ្តើម ផ្លូវ ចេញ ពី ជ្រុង ខាង ស្តាំ បាត សូម បង្វិល ចតុកោណ ដើម្បី ឲ្យ ចំណុច (P,0) ស្ថិត នៅ ផ្នែក ខាង លើ ។ ឥឡូវ នេះ យើង អាច មើល ឃើញ ផ្លូវ ដោយ ដ្យាក្រាម ដូច ខាង ក្រោម ៖
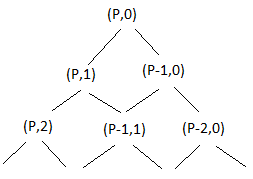
  - ដ្យាក្រាមប្រភេទនេះត្រូវបានគេស្គាល់ថាជាដើមឈើ។ លំនាំ នេះ នឹង បន្ត ធ្វើ ឡើង វិញ រហូត ដល់ យើង បាន ធ្វើ ដំណើរ ពី ( P,0 ) ទៅ ( 0,Q ) ។ នៅ ពេល ដែល វា កើត ឡើង ដើម ឈើ នឹង មាន គ្រប់ ផ្លូវ ដែល អាច ធ្វើ ទៅ បាន ដែល មនុស្ស ម្នាក់ អាច ឆ្លង កាត់ ក្តារ ។
  - ចំនួន វិធី ដើម្បី ទទួល បាន ពី កំពូល (P,1) ទៅ ជា ការ អាក្រាត (I,J) នៅ ក្នុង ដើម ឈើ នេះ គឺ ចំនួន វិធី ដើម្បី ទៅ ដល់ (I-1,J) ហើយ បន្ទាប់ មក ចុះ ទៅ ខាង ស្ដាំ (I,J), បូក នឹង ចំនួន វិធី ដើម្បី ទៅ ដល់(I,J-1) ហើយ បន្ទាប់ មក ចុះ ពី ឆ្វេង ទៅ (I,J)។ និយាយ ម្យ៉ាង ទៀត នេះ គឺ ជា ចំនួន នៅ ក្នុង ត្រីកោណ របស់ ប៉ាស្កាល់ ។
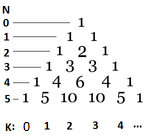
  - ចំនួន នីមួយៗ នៅ ក្នុង ត្រីកោណ របស់ ប៉ាស្កាល់ គឺ ជា ចំនួន សរុប នៃ ចំនួន ពីរ ខាង លើ ។ ចំនួន នៅ ក្នុង ជួរ ឈរ ខាង ឆ្វេង កំពុង រាប់ ជួរ នៃ ក្ដារខៀន ដោយ ចាប់ ផ្តើម ពី 0 ជាមួយ នឹង ក្ដារ ទទេ & # 160; ។ លេខក្រោមត្រីកោណតំណាងឱ្យទីតាំងពីឆ្វេងផងដែរចាប់ផ្តើមពី 0 ផងដែរ។ ចំនួន ជួរ ដេក N'th ក្នុង តំណែង K គឺ ស្មើ នឹង \({N \choose K} = \frac{N!}{(N-K)!K!}\).
  - យើងចង់ស្វែងរកលេខ f(p,q), ដែលចំនួននៃមធ្យោបាយដើម្បីទទួលបានពី (P,0) ទៅ (0,Q)។ ដើម្បី ធ្វើ បែប នេះ ត្រូវ តែ ចេញ ពី កំពូល P times ចុះ ខាង ស្តាំ និង Q ដង នៅ ខាង ឆ្វេង ។ ដោយ ប្រើ រចនា សម្ព័ន្ធ ដើម ឈើ ដែល យើង បាន កំណត់ កាល ពី មុន នេះ គឺ ដូច គ្នា នឹង ការ ធ្វើ ពី ( 0,0 ) ទៅ ( P,Q ) ដែល នៅ ខាង ឆ្វេង និង ខាង ស្តាំ ក្នុង ដើម ឈើ តែ ប៉ុណ្ណោះ ។
  - ទោះ ជា យ៉ាង ណា ក៏ ដោយ នេះ ធ្វើ ឲ្យ យើង ធ្វើ ជំហាន P+Q ដូច្នេះ យើង ស្ថិត នៅ ក្នុង ជួរ P+Q នៅ ក្នុង ដើម ឈើ ។ ដោយ ដឹង ថា យើង បាន ផ្លាស់ ប្តូរ Q ដង ទៅ ខាង ស្តាំ លេខ នៅ ក្នុង ត្រីកោណ ប៉ាស្កាល់ ក្នុង តំណែង នេះ គឺ \({P+Q \choose Q} = \frac{(P+Q)!}{P!Q!}\).
- Proof of Explicit Formula by Induction
  - យើងនឹងបង្ហាញថា រូបមន្តខាងក្រោមគឺស្មើគ្នា។ \[f(P,Q) = \begin{cases}1 & for & P=0 \\1 & for & Q=0 \\f(P,Q-1) + f(P-1,Q) & for & \text{P>0 and Q>0}\end{cases} = \Bigg\{{P+Q \choose Q} = \frac{(P+Q)!}{P!Q!}\]
  - មូលដ្ឋាន អាំង អាំង យ៉ុង ៖ យើងបានដឹងរួចហើយថា f(0,0) = 1 តាមនិយមន័យរូបមន្ត។ បើ យើង ដោត P=0 និង Q=0 ចូល ទៅ ក្នុង រូបមន្ត នោះ យើង ទទួល បាន \(\frac{(0+0)!}{0!0!} = \frac{0!}{1} = 1\). នេះ បង្ហាញ ថា រូបមន្ត មូលដ្ឋាន ស្មើ គ្នា ដែល បញ្ចប់ មូលដ្ឋាន អាំងសុយនីត ។
  - Induction Hypothesis: សូម សន្មត់ ថា រូបមន្ត គឺ ស្មើ នឹង តម្លៃ ទាំងអស់ របស់ P,Q ជាមួយ P+Q = N ។
  - ជំហាន Induction: ដោយ ប្រើ សម្មតិកម្ម នៃ ការ អាំងតេវ យើង បង្ហាញ ពី ភាព ស្មើ គ្នា សម្រាប់ តម្លៃ ទាំង អស់ P,Q ជាមួយ P+Q=N+1 ។ ចំពោះតម្លៃណាមួយ P,Q ជាមួយ P+Q=N+1 យើងមាន 3 ករណីគឺ៖
  - ករណីទី១៖
  - ករណីទី២៖
  - ករណីទី៣៖ \(P,Q > 0\) \[ \begin{align} f(P,Q) &= f(P,Q-1) + f(P-1,Q)\qquad\qquad (+)\\ &= \frac{(P+Q-1)!}{P!(Q-1)!} + \frac{(P-1+Q)!}{(P-1)!Q!}\\ &= \frac{(P+Q-1)!Q}{P!(Q-1)!Q} + \frac{(P-1+Q)!P}{(P-1)!PQ!}\\ &= \frac{(P+Q-1)!}{P!Q!} (Q+P)\\ &= \frac{(P+Q)!}{P!Q!} \end{align} \]
  - (+): ប្រសិនបើ P + Q = N + 1, បន្ទាប់មក P + Q-1 = N, i.e. ដោយ induction hypothesis។
    f(P,Q-1) = \(\frac{(P+(Q-1))!}{(P!(Q-1)!)}\), និងស្រដៀងនឹង f(P-1, Q)
  - នេះ បង្ហាញ ថា រូបមន្ត ទាំង ពីរ សម្រាប់ f(P,Q) ស្មើ គ្នា។
  - ចប់ ភ័ស្តុតាង ។ ∎

តើមានជួរឈរ P និងជួរឈរ Q ខុសគ្នាប៉ុន្មាន?
- គេអាចប្រើរូបមន្តដូចគ្នាសម្រាប់មុខតំណែងទាំងអស់ដែលសមនឹងរាងចតុកោណជាមួយជួរ P-1 និងជួរឈរ Q-1 ដែលជា f (P-1, Q-1) ។

តើមានតំណែងឈ្នះ ឬចាញ់ច្រើនទេ?

ប្រសិនបើទីតាំងមានក្រឡា N នោះអ្នកលេងទី 1 មានជម្រើស N សម្រាប់ការផ្លាស់ប្តូរដំបូង។ ការដែលអាចផ្លាស់ទីដំបូងផ្តល់ឱ្យអ្នកលេងទី 1 នូវអត្ថប្រយោជន៍ ហើយនោះគួរតែមានន័យថាមានមុខតំណែងឈ្នះច្រើនជាងការចាញ់។ នៅក្នុងធាតុមុនវាត្រូវបានបង្កើតឡើងថាតើតំណែងបាត់បង់ប៉ុន្មានក្នុងចំណោមមុខតំណែងដែលមានក្រឡា 2,3,4 ឬ 5 ។ នេះគឺជាលេខមួយចំនួនដែលបញ្ជាក់ពីនិន្នាការដែលទីតាំងដែលមានក្បឿងកាន់តែច្រើន ប្រូបាប៊ីលីតេកាន់តែខ្ពស់ដែលវាជាទីតាំងឈ្នះ។

# នៃក្រឡាក្បឿង	# មុខតំណែង	#បាត់បង់តំណែង	% នៃការបាត់បង់មុខតំណែង
20	627	42	6.69
30	5604	220	3.92
40	37338	1022	2.73
50	204226	4976	2.43
60	966467	20106	2.08
70	4087968	76688	1.87
80	15796476	270142	1.71
90	56634173	897964	1.58

តើមុខងារអ្វីខ្លះនៃអាគុយម៉ង់ 2 '# នៃមុខតំណែង' និង '# នៃការបាត់បង់មុខតំណែង' ផ្តល់តម្លៃប្រហាក់ប្រហែលគ្នាសម្រាប់ជួរនីមួយៗនៃតារាងខាងលើ?
- ចម្លើយត្រូវបានផ្តល់ឱ្យនៅក្នុងធាតុរកឃើញខាងក្រោម។

សម្មតិកម្មដោយ Caribou

មុននេះ យើងបានបង្ហាញថាតំណែងនីមួយៗគឺជាទីតាំងឈ្នះ ឬចាញ់។ ភ័ស្តុតាងបានផ្តល់ឱ្យយើងនូវវិធីសាស្រ្តដោយផ្ទាល់ដើម្បីកំណត់ជំហានមួយជំហានសម្រាប់មុខតំណែងទាំងអស់ថាតើពួកគេចាញ់ឬឈ្នះ។ អ្វីដែលពិសេសនោះគឺវិធីសាស្ត្រនេះមិនត្រូវការការស្វែងរកអ្វីឡើយ (សាកល្បងធ្វើចលនា)។ វាបានរំលឹកយើងអំពី 'Sieve of Eratosthenes' ដើម្បីកំណត់លេខបឋមទាំងអស់រហូតដល់ទំហំមួយចំនួន។

សូមអានអំពី Sieve of Eratosthenes ជាឧទាហរណ៍នៅលើអ៊ីនធឺណិត
- ដើម្បីស្វែងរកលេខបឋមទាំងអស់រហូតដល់ទំហំ N² ដែល N ជាលេខទាំងមូល មួយនឹងធ្វើដូចខាងក្រោម៖
- - A៖ ចាប់ផ្តើមដោយលេខបឋម p=2។
  - B៖ កាត់ផលគុណទាំងអស់នៃ p រហូតដល់ N²។
  - C: ស្វែងរកលេខធំបំផុតបន្ទាប់ > p ដែលមិនទាន់ត្រូវបានកាត់ចេញនៅឡើយ។ ប្រសិនបើលេខនោះជា > N នោះក្បួនដោះស្រាយនឹងឈប់។ បើមិនដូច្នោះទេ សូមទូរស័ព្ទទៅលេខនេះ p ហើយបន្តជាមួយជំហាន B។
- លេខទាំងអស់រហូតដល់ N² ដែលមិនត្រូវបានកាត់ចេញគឺជាលេខបឋមទាំងអស់ < N² ។ មនុស្សម្នាក់អាចរកឃើញការក្លែងធ្វើនៃក្បួនដោះស្រាយនេះនៅលើ https://en.wikipedia.org/wiki/Sieve_of_Eratosthenes

ភាពស្រដៀងគ្នានេះបានបំផុសគំនិតយើងឱ្យគិតអំពីភាពស្រដៀងគ្នាបន្ថែមទៀតរវាងលេខសំខាន់ និងការបាត់បង់តំណែង។ វាបាននាំឱ្យមានសម្មតិកម្មសម្រាប់ការបាត់បង់មុខតំណែងដែលស្រដៀងនឹង 'ទ្រឹស្តីបទលេខបឋម' ។ នេះគឺជាព័ត៌មានលម្អិត។

តារាង៖ ភាពស្រដៀងគ្នារវាងការបាត់បង់តំណែងនៅក្នុង chomp និងលេខសំខាន់៖

លេខ	Chomp
មានចំនួនសរុបជាច្រើនឥតកំណត់។	មានមុខតំណែង Chomp ជាច្រើនគ្មានកំណត់។
មានលេខបឋម និងលេខដែលអាចបំប្លែងបាន។	មានតំណែងចាញ់ និងតំណែងឈ្នះ។
មានលេខបឋមជាច្រើនគ្មានកំណត់។	មានមុខតំណែងបាត់បង់ជាច្រើនឥតកំណត់។
លេខដែលអាចបំប្លែងបាន គឺជាផលនៃចំនួនបឋម និងលេខមួយ។	ទីតាំងឈ្នះគឺជាផលបូកនៃទីតាំងចាញ់ និងទីតាំងមួយ (ព្រោះអ្វីដែលត្រូវបានកាត់ចេញក្នុងចលនាមួយមានរូបរាងនៃជណ្តើរមួយ ហើយដូច្នេះគឺជាទីតាំងមួយ)។
នៅពេលដែលចំនួនបឋមត្រូវបានគេដឹង នោះគេដឹងភ្លាមៗនូវលេខដែលអាចបំប្លែងបានជាច្រើន (គុណទាំងអស់នៃចំនួនបឋម)។	នៅពេលដែលស្គាល់មុខតំណែងចាញ់ នោះគេដឹងភ្លាមៗនូវមុខតំណែងឈ្នះជាច្រើនឥតកំណត់ (មុខតំណែងទាំងអស់ដែលកើតចេញពីការបំពេញចតុកោណកែង រួមទាំងទីតាំងដែលវែងគ្មានកំណត់នៅជួរខាងលើ និងជួរឈរខាងឆ្វេង)។
ចំនួនលេខធំទំនងជាអាចបែងចែកដោយលេខបឋមតូចជាងដោយលេខបឋមធំ។	មុខតំណែងធំទំនងជាអាចកាត់បន្ថយបានចំពោះមុខតំណែងចាញ់តូចជាងការចាញ់ធំ។
ដើម្បីកំណត់ថាតើលេខ N ជាលេខបឋម វាមានប្រសិទ្ធភាពណាស់ក្នុងការដឹងពីលេខបឋមទាំងអស់ P រហូតដល់ឫសការ៉េនៃ N. បន្ទាប់មក គេអាចពិនិត្យមើលថាតើ N អាចត្រូវកាត់បន្ថយទៅ P ដោយការបែងចែក ពោលគឺដោយផ្នែកសាកល្បង N / ទំ។	ដើម្បីកំណត់ថាតើទីតាំង P គឺជាទីតាំងបាត់បង់ វាចាំបាច់ត្រូវដឹងពីទីតាំងបាត់បង់ L ដែលមាននៅក្នុង P. បន្ទាប់មក គេអាចពិនិត្យមើលយ៉ាងមានប្រសិទ្ធភាពថាតើ P អាចត្រូវបានកាត់បន្ថយទៅ L ក្នុងចលនាមួយ។
'Sieve of Eratosthenes' គឺជាមធ្យោបាយដ៏មានប្រសិទ្ធភាពមួយដើម្បីកំណត់លេខបឋមទាំងអស់រហូតដល់លេខ N មួយចំនួន ប៉ុន្តែក៏ដើម្បីពិនិត្យមើលថាតើលេខដែលបានផ្តល់ឱ្យគឺជាលេខបឋមដែរឬទេ។ ក្បួនដោះស្រាយនេះត្រូវបានពិពណ៌នាខាងលើ។	ស្រដៀងគ្នាទៅនឹង 'Sieve of Eratosthenes' មួយចាប់ផ្តើមជាមួយនឹងទីតាំងចាញ់ {1} ហើយឆ្លងកាត់មុខតំណែងឈ្នះទាំងអស់ដែលកាត់បន្ថយទៅទីតាំងចាញ់នោះក្នុងមួយចលនា។ មួយបន្ទាប់មកពិនិត្យមុខតំណែងទាំងអស់ជាមួយនឹងក្បឿងមួយទៀត។ មុខតំណែងទាំងអស់ដែលមិនត្រូវបានកាត់ចេញគឺបាត់បង់តំណែង។
ភាពគ្មានប្រសិទ្ធភាពដែលនៅសល់នៃក្បួនដោះស្រាយ Sieve រួមមានការកាត់ចេញនូវលេខដែលអាចផ្លាស់ប្តូរបានម្តងហើយម្តងទៀត។	ភាពគ្មានប្រសិទ្ធភាពដែលនៅសល់នៃក្បួនដោះស្រាយ sieve រួមមានការឆ្លងកាត់មុខតំណែងដែលឈ្នះម្តងហើយម្តងទៀត។
ដង់ស៊ីតេនៃលេខបឋមថយចុះជាមួយនឹងទំហំរបស់ពួកគេ; ឧ. សមាមាត្រ (# នៃលេខបឋមរហូតដល់ចំនួនទាំងមូល N) / N ថយចុះនៅពេលដែល N កើនឡើង។	ដង់ស៊ីតេនៃការបាត់បង់តំណែងថយចុះជាមួយនឹងទំហំរបស់ពួកគេ; i.e. សមាមាត្រ (# នៃការបាត់បង់មុខតំណែងដែលមានក្រឡារហូតដល់ N) / (# នៃមុខតំណែងទាំងអស់ដែលមានក្រឡា N) ថយចុះនៅពេលដែល N កើនឡើង។ (ការប្រកួតប្រជែង៖ តើរូបមន្តសម្រាប់ការពឹងផ្អែកនៃសមាមាត្រនេះនៅលើ N ហើយតើវាប្រៀបធៀបទៅនឹងរូបមន្តសម្រាប់ដង់ស៊ីតេនៃលេខបឋមយ៉ាងដូចម្តេច?)
ទ្រឹស្តីបទលេខបឋម៖ (# of primes ≤ N) / (N / log(N)) → 1 as N → infinity ។	សម្មតិកម្មអាណាឡូក៖ (# នៃមុខតំណែងជាមួយក្រឡា N) / ((# នៃមុខតំណែងជាមួយក្រឡា N) / កំណត់ហេតុ(# នៃមុខតំណែងជាមួយក្រឡាក្បឿង N)) → 0.283... ជា N → គ្មានដែនកំណត់។

តារាង៖ ភាពខុសគ្នារវាងការបាត់បង់តំណែងនៅក្នុង Chomp និងលេខបឋម៖

លេខ	Chomp
សំណុំនៃលេខទាំងមូលគឺជាសំណុំលំដាប់ទាំងស្រុង; ពោលគឺរវាងលេខទាំងពីរ មួយណាដឹងថាមួយណាធំជាង។	សំណុំនៃមុខតំណែង Chomp ទាំងអស់គឺជាសំណុំដែលបានបញ្ជាដោយផ្នែក។ មុខតំណែងអាចត្រូវបានផ្ទុកទាំងស្រុងនៅក្នុងមុខតំណែងផ្សេងទៀត ប៉ុន្តែមិនចាំបាច់ទេ។
ប្រតិបត្តិការកាត់បន្ថយចំនួនមួយទៅកត្តាសំខាន់មួយរបស់វាគឺការបែងចែក។	ប្រតិបត្តិការដើម្បីកាត់បន្ថយទីតាំងមួយទៅទីតាំងបាត់បង់គឺការដកក្រឡាក្បឿង។
លេខអាចត្រូវបានគេមើលឃើញជាផ្នែកបន្ទាត់នៅលើបន្ទាត់លេខវិមាត្រមួយ។	ទីតាំងត្រូវបានកំណត់តាមរយៈបញ្ជីលេខដែលតម្រៀបតាមទំហំ ហើយដូច្នេះគឺជាវត្ថុ 2D ។

សំណួរបើក៖

តើសម្មតិកម្ម (# នៃមុខតំណែងជាមួយក្រឡា N) / ((# នៃមុខតំណែងជាមួយក្រឡា N) / កំណត់ហេតុ(# នៃមុខតំណែងជាមួយក្រឡាក្បឿង N)) → 0.283... ជា N → ភាពគ្មានទីបញ្ចប់ពិតឬ?

តើអ្នកអាចបញ្ជាក់បានទេ? (យើងមិនទាន់អាចទេ :-))

ហ្គេម Chomp ដែលលេងខាងលើគឺជាកំណែ 2D Chomp ។ នេះមានន័យថាក្តារនោះមានទំហំតែ2 ប៉ុណ្ណោះមានទទឹងនិងកម្ពស់។

តើអ្នកអាចស្រមៃមើលកំណែ 3D Chomp បានទេ?
- វិធីសាមញ្ញបំផុតក្នុងការស្រមៃបន្ថែមវិមាត្រថ្មីទៅក្នុងហ្គេមគឺដោយបន្ថែមវិមាត្រទីបីទៅក្តារ។ ជំនួសឱ្យតែទទឹង និងកម្ពស់ ក្តារថ្មីនឹងមានប្រវែង ទទឹង និងកម្ពស់។ ប្រសិនបើនរណាម្នាក់មានគូបតូចៗសម្រាប់លេងជាមួយ ដូចជាគ្រាប់ឡុកឡាក់ ពួកគេអាចលេងហ្គេម 3D នេះដូចបង្ហាញក្នុងរូបភាពខាងក្រោម។
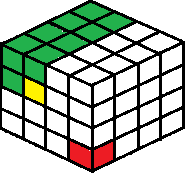
- នៅពេលធ្វើចលនា មនុស្សម្នាក់នឹងដកគូបដែលបានជ្រើសរើស ក៏ដូចជារាល់គូបទៅខាងឆ្វេង ខាងលើ និងផ្នែកខាងលើនៃគូបដែលបានជ្រើសរើស។ ការផ្លាស់ទីគំរូមួយត្រូវបានបន្លិចជាពណ៌លឿងនៅក្នុងរូបភាព ដែលក៏លុបក្រឡាពណ៌បៃតងទាំងអស់នៅក្នុងរូបភាពផងដែរ។ អ្នកដែលយកក្បឿងចុងក្រោយដែលបង្ហាញដោយក្បឿងពណ៌ក្រហមនៅក្នុងរូបភាពគឺជាអ្នកលេងដែលចាញ់ហ្គេម។
- ដើម្បីធ្វើឱ្យការលេងហ្គេមកាន់តែងាយស្រួលជាមួយគូបពិត មនុស្សម្នាក់អាចរុញគូបទល់នឹងជ្រុងមួយ ដូចជាជ្រុងនៃប្រអប់ស្បែកជើង ដូច្នេះថាក្បឿងពណ៌ក្រហមស្ថិតនៅជ្រុងនៃប្រអប់ ហើយអាចចូលប្រើបានតែម្តងគត់។ ត្រូវបានដកចេញផងដែរ។ ការប្រើប្រអប់វាមិនចាំបាច់ទេ ប៉ុន្តែវានឹងធ្វើឱ្យគូបមានស្ថេរភាព និងធ្វើឱ្យវាកាន់តែងាយស្រួលក្នុងការយកគូបចេញដោយមិនធ្វើឱ្យខូចរចនាសម្ព័ន្ធទាំងមូល។

ចុះយ៉ាងណាចំពោះការលេង Chomp ក្នុងទំហំកាន់តែច្រើន?
- មុននេះ យើងបានកំណត់ថាវាងាយស្រួលគ្រប់គ្រាន់ក្នុងការបន្ថែមវិមាត្រថ្មីទៅក្នុងហ្គេម Chomp ។ ប្រសិនបើនរណាម្នាក់ចង់លេង Chomp ក្នុងវិមាត្រខ្ពស់ជាង 3D នោះពួកគេនឹងបន្តបន្ថែមវិមាត្រថ្មីទៅក្នុងបន្ទះ Chomp ។ ទោះយ៉ាងណាក៏ដោយបន្ទាប់ពី 3D មិនមានវិធីដើម្បីក្លែងធ្វើបន្ទះ Chomp ដោយប្រើប្លុកទៀតទេ។ ទោះយ៉ាងណាក៏ដោយ មានវិធីមួយដើម្បីក្លែងធ្វើហ្គេម chomp ដោយប្រើខ្មៅដៃ និងក្រដាស ហើយវិធីសាស្ត្រនេះអនុញ្ញាតឱ្យយើងលេងហ្គេមក្នុងគ្រប់ទំហំ មិនមែនត្រឹមតែ 2D ឬ 3D នោះទេ។
- យើងនឹងចាប់ផ្តើមដោយការលេងហ្គេម 2D Chomp នៅលើក្រដាស។ វិធីមួយដែលអាចក្លែងធ្វើហ្គេមគឺដោយជ្រើសរើសលេខដំបូងដែលមានកត្តាសំខាន់ពីរផ្សេងគ្នា។ ឧទាហរណ៍ 72 = 2³ x 3² ។ បន្ទាប់មកយើងសរសេរកត្តាទាំងអស់នៃចំនួននេះក្នុងទម្រង់ជាចតុកោណដូចបានបង្ហាញខាងក្រោម។
- 72 36 18 9
  24 12 6 3
  8 4 2 1
- លេខដែលនៅជិតខាងស្ដាំណាមួយតូចជាងដោយកត្តា 2 ហើយលេខជិតខាងណាមួយនៅខាងក្រោមគឺតូចជាងដោយកត្តា 3។ ដើម្បីផ្លាស់ទីនៅលើក្តារនេះ មួយនឹងជ្រើសរើសលេខមួយ។ បន្ទាប់មក អ្នកនឹងដកលេខនោះចេញ រួមជាមួយនឹងកត្តាណាមួយរបស់វា។ អ្នកណាយកលេខ 72 ចាញ់ហ្គេម។
- ដើម្បីឱ្យមានចតុកោណកែងដំបូងធំជាង គេអាចរកឃើញលេខធំជាងដោយប្រើរូបមន្ត 2^P x 3^Q ។ ដោយការជំនួស P និង Q ជាមួយនឹងលេខធំជាងនេះ មួយនឹងទទួលបានក្តារធំ និងធំជាងសម្រាប់ 2D Chomp ។
- តើមនុស្សម្នាក់អាចធ្វើការក្លែងធ្វើបែបនេះសម្រាប់វិមាត្រខ្ពស់ដោយរបៀបណា?
  - ដើម្បីពង្រីកកំណែខ្មៅដៃ និងក្រដាសរបស់ Chomp ពី 2D ទៅ 3D អ្នកគ្រាន់តែត្រូវការពង្រីករូបមន្តដែលប្រើដើម្បីស្វែងរកលេខចាប់ផ្តើម។ ជំនួសឱ្យការជ្រើសរើសលេខដែលមានកត្តាសំខាន់ 2 ផ្សេងគ្នា មួយនឹងជ្រើសរើសលេខដែលមានកត្តាសំខាន់ 3 ផ្សេងគ្នា។ យើងអាចប្រើរូបមន្តថ្មីដើម្បីរកលេខនេះដូចខាងក្រោម៖ 2^P x 3^Q x 5^R ។ បន្ទាប់មកដោយប្រើវិធីសាស្រ្តដូចពីមុន ហ្គេមអាចត្រូវបានក្លែងធ្វើជា 3 វិមាត្រ។ ការចូលទៅកាន់ទំហំធំជាងនេះ គឺតម្រូវឱ្យបន្ថែមលេខសំខាន់ថ្មីទៅក្នុងរូបមន្ត អាស្រ័យលើចំនួនវិមាត្រដែលអ្នកចង់បាន។