300000
English | Français | فارسی | 中文 | Українська | Azerbaijani | ខ្មែរ | Tiếng Việt | Bahasa Melayu | Deutsch | O'zbek | РусскийSliding Blocks ©©
Total number of plays: 415797
Total number of wins: 307310
Total number of wins: 307310
How To Play
- To win, move the yellow block to the exit.
- To move a block, click and drag it, or click the block then click on the empty space.
- Grey blocks cannot be moved.
Puzzles shown on this page are created and owned by Caribou Contests ©
Editor Instructions
- Use the width and height labels to change the size of your board.
- Select a colour below the board to choose what colour block you wish to put on the board.
- Click on the board to place a single block of that colour.
- Click and drag on the board to enlarge the size of a block.
- Click the 'Clear Board' button to clear your board and start over.
- Click 'Generate Random Board' to randomly create a puzzle to edit.
- Click the 'Play Your Puzzle' button when you wish to play your board.
- Click 'Discard Your Puzzle' to cancel editing and return to the normal game.
Moves made: 0
Width: Height:
Difficulty: Easy Medium Hard Very Hard Famous
SlowFast
Bạn hưởng lợi nhiều nhất từ các hoạt động bằng cách suy nghĩ một lúc trước khi mở rộng câu trả lời cho những câu hỏi.
Chúc bạn vui vẻ.
Sau khi chơi "Sliding Blocks" được một thời gian, trò chơi này có sự tương đồng với trò chơi nào khác của chúng tôi?
- Trò chơi "Sokoban" có sự tương đồng với "Sliding Blocks" vì một số lí do.
-
Bạn thấy được những điểm nào tương đồng?
- Trong cả hai trò chơi:
-
- Một đồ vật phải được di chuyển xung quanh, và vấn đề là sự thiếu sót khoảng trống.
- Trình tự giải quyết có thể sẽ dài.
- Cây tìm kiếm hẹp. Điều này có nghĩa là nếu một người thực hiện một di chuyển ngẫu nhiên không có kế hoạch, thì người đó sẽ sớm quay trở lại vị trí người đó đã gặp trước đây. Điều đó khiến câu đố này dễ hơn rất nhiều so với, để lấy làm ví dụ, một khối Rubik, khi mà một di chuyển ngẫu nhiên sẽ về cơ bản sẽ không bao giờ đưa bạn trở lại vị trí ban đầu.
- Nó rất hữu ích để lập ra những mục tiêu trung gian. Điều này sẽ được nói thêm ở bên dưới.
Một người có thể sửa đổi một câu đố "Sliding Blocks" như thế nào để nó trở thành dễ hoặc khó hơn?
- Để sửa đổi một câu đố một người có thể ấn vào "Create a Puzzle". Một câu đố sẽ trở thành dễ hơn nếu các khối được thay thế bởi các khoảng trống, hoặc nếu các khối to được chia thành các khối nhỏ hơn nhưng vẫn chiếm từng đó không gian, hoặc khi các khối màu xám bất động bị biến thành các khối màu xanh để trở thành có thể di chuyển được. Tương ứng, một câu đố trở thành khó hơn nếu khoảng trống bị chiếm bởi một khối mới, hoặc các khối nhỏ hợp thành các khối lớn hơn, hoặc khối màu xanh bị biến thành khối màu xám.
Khi xem những lời giải dưới dạng hoạt hình cho các câu đố, bạn có thể quan sát một qui tắc chung mà các lời giải này đều có mà có thể là một gợi ý tốt cho những nỗ lực tìm lời giải của riêng bạn không?
- Tiếp theo, một gợi ý sẽ được đưa ra.
Khi vặn chìa trong ổ khoá trở nên khó khăn hơn, hoặc khi xích xe đạp của bạn bị cứng, thì bạn sẽ làm gì?
- Bạn có thể bôi dầu hoặc mỡ bôi trơn để làm giảm ma sát.
Trong trò "Sliding Blocks" chúng ta cũng muốn di chuyển những khối xung quanh và dường như gặp phải một loại ma sát nào đó. Có cách giải quyết nào tương tự ở đây không?
- Vai trò của mỡ bôi trơn ở đây được thực hiện bởi các khối nhỏ. Bạn nên có 2 hoặc đôi khi là 3 khối nhỏ ở giữa hai khối lớn hơn, đặc biệt là xung quanh khối màu vàng, khối cần được di chuyển nhiều nhất. Dưới đây là minh chứng.
- Giả sử rằng khối màu vàng rộng bằng hai ô vuông nhỏ và cần được di chuyển xuống dưới.
- Sau đó, trước khi di chuyển, phải có hai khoảng trống bên dưới hình khối, và sau khi di chuyển sẽ có hai khoảng trống ở nơi khối từng nằm. Sau đó, hai khoảng trống nằm phía trên khối vàng cần phải được di chuyển lần nữa xung quanh khối vàng để khối này có thể di chuyển xa hơn. Để có thể di chuyển hai khoảng trống xung quanh khối màu vàng, các khối xung quanh cũng cần phải di chuyển được. Các khối nhỏ dễ di chuyển hơn các khối lớn, chẳng hạn như ở quanh các góc. Thế nên nên có các nhóm gồm 2 hoặc đôi khi là 3 khối nhỏ nằm giữa các khối lớn, đặc biệt là ở xung quanh khối màu vàng, khối cần được di chuyển nhiều nhất.
- Hãy xem các giải pháp cho các vấn đề khó và kiểm tra xem tần suất áp dụng của lời khuyên phía trên.
Để tìm được chuỗi giải pháp dài, nó sẽ hữu ích khi nghĩ về các chuỗi giải pháp ngắn như các khối xây dựng mà từ đó các chuỗi dài hơn được tạo thành. Một bài tập cơ bản cho một chuỗi ngắn như vậy là xoay các khối theo hình tròn. Bạn có thể nghĩ thực hiện việc này như thế nào không?
- Ví dụ, hãy xem xét vị trí sau:
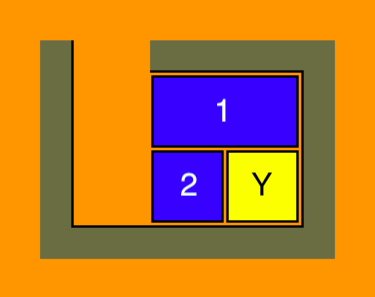
- Các khối 1, 2 và Y, và hai khoảng trống có thể được di chuyển xung quanh trong một vòng tròn, và do đó, khối số 1 hoặc hai không gian trống có thể được đặt ở bất cứ nơi nào cần thiết.
- Vị trí tiếp theo có hai khối lớn hơn là khối 1 và 3, nhưng cũng có nhiều khoảng trống hơn:
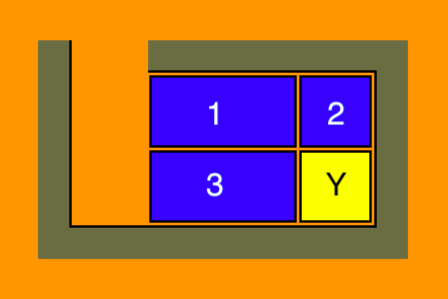
- Ở đây tất cả các khối cũng có thể được di chuyển theo hình tròn, điều này cho phép chúng ta di chuyển các khối 1, 3 và các khoảng trống tới bất cứ nơi nào cần thiết.
- Cả hai chuyển động tròn sẽ là cần thiết trong một ví dụ được mô tả thêm dưới đây.
Có phải chỉ có những khối màu xanh dương và vàng được di chuyển xung quanh không?
- Để nói chính xác, thì đúng là như vậy. Nhưng trong khoa học, sự linh hoạt và sáng tạo được coi là điều tốt. Hay là chúng ta coi những khoảng trống cũng như các khối có khả năng đặc biệt là chúng có thể thay đổi vị trí với các khối lân cận? Lấy làm ví dụ, trong vật lý chất rắn, các electron bị thiếu trong một mạng lưới nguyên tử để lại chỗ trống và chỗ trống như vậy chuyển động như một hạt thật chỉ là với điện tích trái dấu. Khi nghĩ theo cách này, sẽ dễ dàng hơn cho bạn để giải thích, chẳng hạn như trong trường hợp giải thích cách thức hoạt động của một bóng bán dẫn.
- Trong trò chơi của chúng tôi, hai chuyển động tròn của các khối được đề cập trong phần trước cũng có thể được nhìn nhận như chuyển động tròn của hai khoảng trống theo hướng ngược lại.
Nếu "Sokoban" và "Sliding Blocks" giống nhau, vậy thì chiến lược giải đố nào của "Sokoban" có thể được sử dụng trong "Sliding Blocks"?
- Bởi vì cây tìm kiếm trong cả hai trò chơi đều khá hẹp nên trong cả hai trò chơi đều có thể chia toàn bộ giải pháp thành các mục tiêu trung gian. Ví dụ, hãy xem xét câu đố sau:
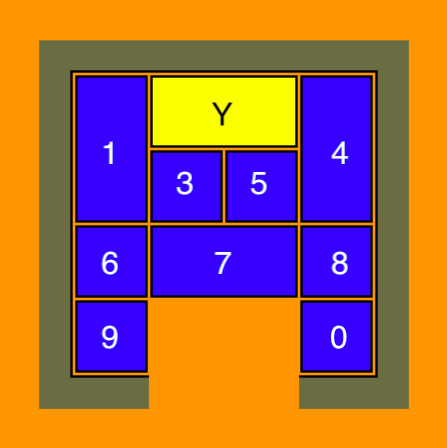
- Khối rộng màu vàng tên Y phải vượt qua khối rộng số 7 để có thể đi ra ngoài. Làm thế nào để điều đó có thể xảy ra? Để Y có thể di chuyển xuống dưới, chúng ta cần các khối nhỏ xung quanh Y để sau khi di chuyển Y lần đầu tiên, khoảng trống phía trên Y có thể được di chuyển xuống bên dưới Y để Y có thể di chuyển thêm xuống dưới. Do đó hai khối nhỏ phải được đưa vào giữa Y và khối 1 hoặc 4, vầ sau đó khoảng trống cần được tạo ở bên dưới Y. Y sau đó được di chuyển xuống dưới và 2 khối nhỏ sẽ được di chuyển để tạo khoảng trống ở trên Y.
- Trước khi thực hiện tất cả những điều đó, 1 hoặc 4 do đó phải được di chuyển xuống dưới. Chúng ta hãy đi với khối 1. Để di chuyển khối 1 xuống, các khối 6 và 9 phải được di chuyển ra khỏi đường đi. Dựa vào những gợi ý trước đó, để các khối nhỏ ở gần khối màu vàng, chúng ta nên bắt đầu bằng việc di chuyển khối số 7 xuống, khối 6 và 9 di chuyển vào khoảng trống mới mở ở trên số 7, và rồi sau đó di chuyển 1 xuống và giờ xoay Y và 3 và 5 theo hình tròn như đã được mô tả trước đó để Y và 3,5 đổi chỗ cho nhau. Sau khi tất cả những hành động trên xảy ra, chúng ta sẽ có vị trí kết quả sau:
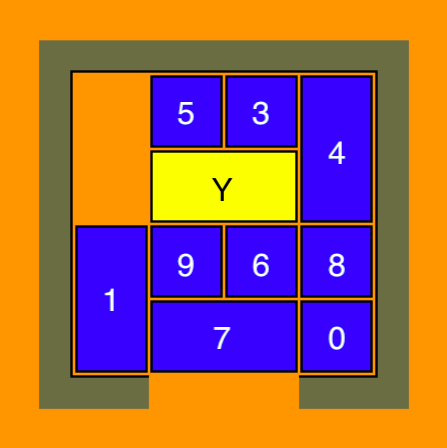
- Giờ chúng ta có thể di chuyển 1 lên, hoặc di chuyển 5,3 và Y sang bên trái, và di chuyển những khối khác sang lên trên về phía bên phải. Vì việc đưa các khổi lớn hơn vượt qua dọc theo nhau luôn luôn khó hơn, chúng ta nên nhân cơ hội để di chuyển khối số 1 lên. Việc còn lại cần làm là di chuyển 9,6 sang bên trái để di chuyển Y xuống, di chuyển 3 xuống dưới 5, và 4 sang bên trái để 8,0 có thể đi lên. Giờ đây, việc "luân chuyển các khối xây dựng" như đã được miêu tả phía trên được dùng để đưa Y lên trên lối thoát. Câu đố đã được giải.
Sơ lược
- Theo chiến thuật chung, hãy bắt đầu từ mục tiêu cuối cùng là lấy khối màu vàng ra và sau đó đi ngược lại và xây dựng nhưng mục tiêu phụ, mục tiêu phụ-phụ,... cần thiết, mà những mục tiêu đó cùng nhau sẽ tiết lộ toàn bộ lời giải.
- Di chuyển các khối lớn ra khỏi đường đi, lý tưởng nhất là vào một góc cách xa lối thoát.
- Thường rất dễ để quan sát được một số khối quá to để có thể vượt qua nhau. Bằng cách nhận thức được rằng những di chuyển có hạn chế, một người có thể tránh được việc đoán và tránh những nỗ lực vô ích và tạo ra các mục tiêu phụ tốt hơn.
- Để một khối to có thể tiếp tục di chuyển, khoảng trống cần được tạo ra ở phía trước khối, sau đó khối được di chuyển dẫn đến các khoảng trống đằng sau khối. Những không gian trống này cần được "di chuyển" lên phía trước khối to để có thể tiếp tục di chuyển khối to xa hơn. Đối với tất cả các chuyển động đó, cần thiết có các khối nhỏ ở trước và sau các khối to. Vì vậy, chuỗi di chuyển đầu tiên có thể chỉ nhằm mục đích đặt các khối nhỏ ở nơi sẽ cần chúng sau này, ở xung quanh các khối to hơn.
- Để di chuyển một khối lớn, cần phải có không gian theo hướng nó sẽ được di chuyển. Ví dụ: nếu khối có chiều rộng 2 theo một hướng nhưng toàn bộ câu đố chỉ có một không gian trống thì khối đó sẽ không bao giờ được di chuyển theo hướng này mà có thể di chuyển theo hướng vuông góc với hướng mà nó mỏng hơn. Tương tự, nếu một câu đố chỉ có 2 khoảng trống và một khối có chiều rộng là 3 thì khối này sẽ không bao giờ được di chuyển theo hướng vuông góc của chiều rộng đó vì đối với 3 khoảng trống đó sẽ là cần thiết. Nhưng khối có thể di chuyển theo hướng khác. Một lần nữa, biết khả năng di chuyển hạn chế giúp dễ dàng tìm ra giải pháp hơn bằng cách nhận thức được hướng nào mỗi khối lớn hơn chỉ có thể được di chuyển và chỉ nghĩ đến những động thái như vậy.
- Sẽ rất hữu ích khi 'xem' các vòng tròn trong đó một hoặc hai khoảng trống được di chuyển trong một vòng tròn cùng với tất cả các hộp trong vòng tròn. Một vòng tròn như vậy có thể có hình dạng của một hình chữ nhật. Di chuyển mọi thứ (không gian trống và hộp) trong vòng tròn không chạm vào bất kỳ khối nào khác bên ngoài vòng tròn và có vẻ vô nghĩa. Nhưng tác dụng phụ của việc đưa các khối nhỏ đến một vị trí nhất định trong vòng tròn có thể rất quan trọng sau này. Một ví dụ sẽ là một nơi gần một khối lớn để lấp đầy các khoảng trống sau khi khối này được di chuyển. Suy nghĩ về các chuỗi di chuyển như vòng tròn thay vì các bước di chuyển đơn lẻ cho phép người ta suy nghĩ sâu sắc hơn.
- Một chiến lược học tập được khuyến nghị là hãy bắt đầu với những câu đố dễ và tăng dần độ khó lên. Nếu một người không thể giải một câu đố thì người đó sẽ xem một lời giải dưới dạng hoạt hình trong chế độ chuyển động chậm, tìm nước đi mà người đó đã bỏ lỡ, nghĩ về mục đích của nước đi đó bằng cách xem những nước đi tiếp theo, và làm thế nào một người có thể nhìn được mục đích này.
Theo dõi cập nhật sắp tới