300000
English | Français | فارسی | 中文 | Українська | Azerbaijani | ខ្មែរ | Tiếng Việt | Bahasa Melayu | Deutsch | O'zbek | РусскийSliding Blocks ©©
Nombre total de parties: 415797
Nombre de victoires: 307310
Nombre de victoires: 307310
Comment Jouer
- L’objectif est de sortir le bloc jaune du plateau.
- Pour déplacer un bloc, il suffit de cliquer là-dessus et de le faire glisser. Vous pouvez aussi cliquer sur le bloc et ensuite cliquer sur l’espace vide adjacent.
- Les blocs gris ne peuvent pas être déplacés.
Les casse-têtes qui figurent sur cette page sont les créations et la propriété des Concours Caribou ©
Éditeur : Mode d’Emploi
- Redimensionnez le plateau en modifiant les valeurs de Longueur et Largeur.
- Sélectionnez une couleur sous le plateau pour choisir quelle sorte de bloc vous voulez poser sur le plateau.
- Cliquez sur le plateau pour y poser un seul bloc de la couleur sélectionnée.
- Cliquez et faites glisser votre curseur pour élargir le bloc.
- Cliquez sur le bouton ‘Effacer’ pour effacer le plateau et recommencer.
- Cliquez sur ‘Générer un Plateau Aléatoire’ pour générer un casse-tête aléatoire à modifier.
- Cliquez sur ‘Jouer à votre Casse-Tête’ quand vous voulez jouer le plateau créé.
- Cliquez sur ‘Abandonner votre Casse-Tête’ pour annuler vos modifications et retourner au jeu normal.
Nombre de coups effectués : 0
Largeur : Longueur :
Niveau de Difficulté : Facile Moyen Difficile Très Difficile Célèbre
Vitesse : LenteRapide
Pour profiter au mieux des activités, il est préférable de réfléchir par vous-même avant de dévoiler les réponses.
Amusez-vous!
Après avoir joué à Sliding Blocks pendant un bon moment, à quel autre jeu de notre site ressemble-t-il?
- Le jeu Sokoban ressemble à Sliding Blocks.
-
Quelles similitudes avez-vous relevées entre ces deux jeux?
- Dans les deux jeux:
-
- Il faut déplacer quelque chose, et le problème est le manque d’espace vide.
- Les séquences de solution peuvent être longues.
- L’arbre de recherche est ‘étroit’, ce qui signifie que si on joue des coups au hasard sans stratégie, on revient sous peu à une position qu’on a déjà rencontrée. Du coup, c’est ce qui rend ces casse-têtes plus faciles qu’un Rubik’s cube, où il est alors très improbable de retrouver la position de départ en effectuant des coups au hasard.
- Il est utile de se fixer des objectifs intermédiaires, qu’on abordera plus tard dans le texte ci-dessous.
Comment peut-on modifier un casse-tête Sliding Blocks pour le rendre plus facile ou plus difficile?
- Pour modifier un casse-tête, on peut cliquer sur ‘Modifier le Plateau Actuel’. Un casse-tête devient plus facile si on remplace des blocs par de l’espace vide, si on remplace un grand bloc par de plus petits blocs occupant la même place, et si on remplace des blocs gris fixes par des blocs bleus qu’on peut déplacer. De même, un casse-tête devient plus difficile si on réduit l’espace vide en plaçant des blocs, si on combine des petits blocs pour former des blocs plus grands, et si on remplace un bloc bleu par un bloc gris.
En regardant des solutions animées des casse-têtes, observez-vous un principe de résolution général qui pourrait vous servir quand vous tentez de résoudre les casse-têtes?
- Un indice suivra.
Que faites-vous lorsqu’il devient difficile de tourner une clé dans une serrure, ou lorsque la chaîne de votre vélo se bloque?
- Vous pouvez lubrifiez avec de l’huile ou de la graisse pour réduire la friction.
Dans Sliding Blocks aussi on veut déplacer des blocs mais il semble qu’on rencontre une sorte de friction. Existe-t-il une solution pareille?
- Ici ce sont les petits blocs qui lubrifient. C’est une bonne idée de placer deux ou parfois 3 petits blocs entre deux grands blocs, spécialement autour du bloc jaune qui est le plus souvent déplacé. Voici la justification.
- Disons que le bloc jaune fait deux cases de largeur et qu’il faut le descendre sur le plateau.
- Alors, avant qu’on le déplace il faut deux cases vides en dessous, et après qu’on l’aura déplacé il y aura deux cases vides où se trouvait le bloc jaune avant. Ensuite, pour pouvoir descendre le bloc jaune de nouveau, il faut que ces cases vides se déplacent autour de lui. Pour déplacer les cases vides autour du bloc jaune, les blocs qui l’entourent doivent être mobiles. Il est plus facile de déplacer un petit bloc, autour d’un coin par exemple. Donc, c’est une bonne idée de faire en sorte qu’il y ait des groupes de 2 ou même 3 petits blocs entre les grands blocs, spécialement autour du bloc jaune qui est le plus souvent déplacé.
- Jetez un oeil à des solutions de problèmes difficiles et vérifier à quelle fréquence la recommandation ci-dessus est applicable.
Pour trouver de longues séquences de solution, il est utile de penser aux longues séquences comme étant composées de petites séquences. Souvent l’objet d’une telle petite séquence consiste à faire tourner des blocs dans un cercle. Pouvez-vous envisager cette action?
- Comme exemple, on peut considérer la position suivante:
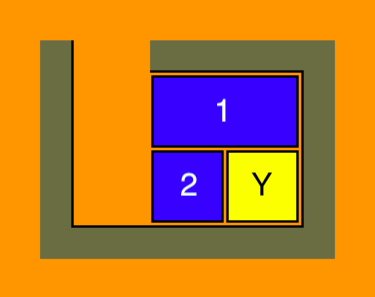
- On peut faire tourner les blocs 1, 2, Y, et les deux cases vides dans un cercle, et ainsi placer le bloc 11 et les deux cases vides où il convient.
- La position suivante comprend deux blocs plus grands (1 et 3) mais plus de place aussi:
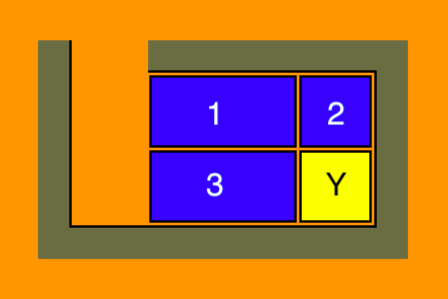
- Ici aussi on peut faire tourner tous les blocs dans un cercle, ce qui nous permet de placer les grands blocs et les cases vides où il convient.
- On aura besoin des deux mouvements circulaires décrits dans un exemple qui sera énoncé par la suite.
Est-ce que seuls les blocs bleus et jaunes sont mobiles?
- À proprement parler, oui. Pourtant, en sciences, il est bien d’avoir une souplesse et une ouverture d’esprit. Et si on considérait les cases vides comme des blocs qui ont la propriété spéciale de pouvoir échanger leur place avec celle des blocs avoisinants? Par exemple, dans le domaine de la physique de l’état solide, les électrons manquants dans une grille d’atomes laissent un vide et un tel vide se déplace comme une vraie particule mais de charge opposée. Penser ainsi peut rendre plus facile, par exemple, l’explication du fonctionnement d’un transistor.
- Dans notre jeu, on pourrait représenter les deux mouvements circulaires des blocs mentionnés ci-dessus comme le mouvement circulaire des cases vides dans le sens contraire.
Si Sokoban et Sliding Blocks se ressemblent, alors quelles stratégies de résolution applicables pour Sokoban peuvent servir dans Sliding Blocks?
- Du fait que l’arbre de recherche des deux jeux est étroit, il est donc possible de diviser la solution en plusieurs objectifs intermédiaires. Considérez le casse-tête suivant:
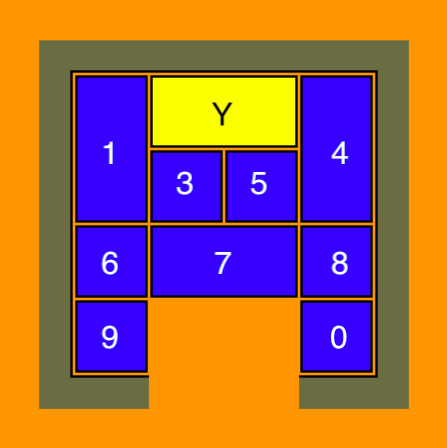
- Le grand bloc Y doit franchir le grand bloc 7 afin de sortir. Comment faire? Pour que Y puisse descendre, il faut qu’il y ait des petits blocs autour de lui: ainsi, une fois qu’on l’aura déplacé une première fois, on pourra déplacer l’espace vide au-dessus de lui en-dessous, pour pouvoir le descendre davantage. Alors on devrait faire en sorte qu’il y ait des petits blocs entre Y et un bloc (soit 1, soit 4) et ensuite qu’il y ait de l’espace vide sous lui. Ensuite on pourrait descendre Y et on devrait mettre les 2 petits blocs dans l’espace vide au-dessus de lui.
- Pour accomplir cela, il faut dans un premier temps faire descendre 1 ou 4. Procédons avec 1. Pour que 1 puisse descendre, il faut déplacer les blocs 6 et 9 de façon à ce qu’ils ne bloquent plus le chemin. En se rappelant de notre astuce qui dit qu’il est avantageux de mettre les petits blocs autour du bloc jaune, il faut d’abord faire descendre le bloc 7, placer les blocs 6 et 9 dans l’espace vide au-dessus de 7, ensuite faire descendre le bloc 11, puis faire tourner les blocs Y, 3, et 5 dans un cercle de sorte que Y échange sa place contre celles de 3 et 5. Cela accompli, la position résultante sera:
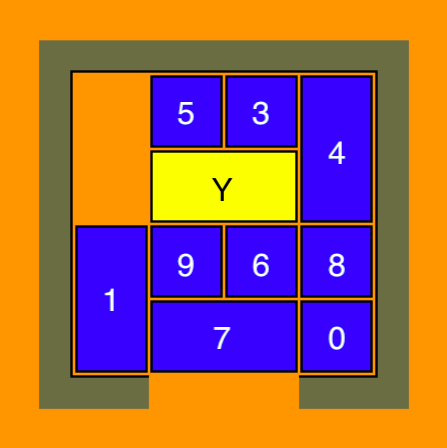
- Arrivé à cette étape, on peut soit faire monter le bloc 1, soit déplacer 5,3 et Y vers la gauche et déplacer les autres blocs placés du côté droit. On devrait utiliser l’opportunité de faire monter 1 car il est toujours plus difficile de manipuler deux grands blocs avoisinants. Tout ce qui nous resterait à faire, serait de déplacer 9,6 vers la gauche pour faire descendre Y, de déplacer 3 sous 5, et déplacer 4 vers la gauche pour pouvoir faire monter 8,0. À partir de là, on pourrait effectuer la rotation de blocs décrite ci-dessus pour placer Y au-dessus de la sortie. Le casse-tête est résolu.
Sommaire
- Comme stratégie générale, il vaut mieux commencer par l'objectif final de faire sortir le bloc jaune, puis revenir en arrière et formuler les sous-, sous-sous-,... objectifs nécessaires qui, ensemble, révéleront toute la solution.
- Si possible, il est utile de déplacer les gros blocs pour libérer le chemin vers la sortie, de préférence dans un coin éloigné de la sortie.
- Il est souvent facile de voir que certains blocs sont trop gros pour pouvoir se croiser. En restant conscient de ces limitations de déplacement, on peut éviter de deviner et de tenter des tentatives infructueuses et ainsi mieux formuler les sous-objectifs.
- Pour continuer de déplacer un bloc plus grand, des espaces vides doivent être créés devant le bloc, puis le bloc est déplacé, ce qui crée des espaces vides derrière le bloc. Ces espaces vides résultants doivent être "déplacés" vers l'avant du gros bloc pour déplacer le gros bloc plus loin. Pour permettre ces déplacements, de petits blocs sont nécessaires devant et derrière les gros blocs. Ainsi, la première séquence de mouvements peut simplement viser à placer les petits blocs là où ils seront nécessaires plus tard, autour de blocs plus gros.
- Pour déplacer un gros bloc, il doit y avoir de l'espace dans la direction dans laquelle il doit être déplacé. Par exemple, si le bloc a une largeur de 2 dans une direction mais que l'ensemble du casse-tête n'a qu'un seul espace libre, alors ce bloc ne sera jamais déplacé dans cette direction mais pourra être mobile dans une direction perpendiculaire où il est moins large. De même, si un casse-tête n'a que 2 cases libres et qu'un bloc a une largeur de 3 alors ce bloc ne sera jamais déplacé dans le sens perpendiculaire à cette largeur car pour cela 3 cases libres seraient nécessaires. Mais le bloc peut être mobile dans l'autre sens. Encore une fois, le fait de connaître la mobilité limitée facilite la recherche d'une solution en sachant dans quelle direction chaque bloc plus gros ne peut être déplacé et en ne pensant qu'à ces mouvements.
- Il est utile de "visualiser" les cercles où un ou deux espaces vides sont déplacés dans un cercle avec toutes les cases du cercle. Un tel cercle peut avoir la forme d'un rectangle. Tout déplacer (espaces libres et cases) dans le cercle ne touche aucun autre bloc en dehors du cercle et peut sembler inutile. Mais l'effet secondaire d'amener de petits blocs à une certaine position dans le cercle peut être crucial pour la solution plus tard. Un exemple serait un endroit près d'un gros bloc pour remplir les espaces vides après le déplacement de ce bloc. Penser en termes de séquences de mouvements comme des cercles au lieu de déplacements simples permet de réfléchir plus profondément.
- Une stratégie d'apprentissage recommandée consiste à commencer par des casse-têtes faciles et à augmenter lentement le niveau de difficulté. Si l'on ne peut pas résoudre une énigme, on regarde la solution animée au ralenti, on trouve le coup manqué, on réfléchit au but de ce coup en regardant les coups suivants, et à la façon dont on aurait pu voir ce but.
Suivez ou abonnez-vous à l'Infolettre