300000
English | Français | فارسی | 中文 | Українська | Azerbaijani | ខ្មែរ | Tiếng Việt | Bahasa Melayu | Deutsch | O'zbek | РусскийFruit Salad©
Total number of plays: 379532
Total number of wins: 131385
Total number of wins: 131385
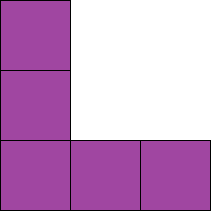
How to Win: Move each blind from the right board onto one quadrant of the left board so that the only fruits visible match those shown above the board.
How to Play: Click on a blind on the right board to select it. Once selected, you can move a blind by dragging it with your mouse or touch screen, and you can click on the buttons below the board to flip or rotate it. When you think you’ve found the solution, click ‘Submit’ to check your answer.
Note You can use keyboard controls instead (click ‘Show Keyboard Controls’ to display them). If you find the animations distracting, click ‘Turn Animations Off’.
| W or UP Arrow Key: Move the selected blind up. | S or DOWN Arrow Key: Move the selected blind down. |
| A or LEFT Arrow Key: Move the selected blind to the left. | D or RIGHT Arrow Key: Move the selected blind to the right. |
| Q: Rotate the selected blind counter-clockwise. | E: Rotate the selected blind clockwise. |
| F: Flip the selected blind. | R: Reset the board. |
| Enter: Submit your answer. | T: Cycle to the next blind. |
Beginner Question:
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
Intermediate Question:
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
Expert Question:
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
You get the most out of the activities by first thinking for a while before expanding the answers to the questions. Have fun.
What are some strategies to use when solving a Fruit Salad puzzle?
-
In this section, "checking a blind" refers to when you place a blind somewhere on the board and rotate/flip it through all its orientations. Keep track of what is visible each time, and check if these fruits are a part of the solution.
- Hint #1: Find the sections where a specific blind can go. This can be done by checking the same blind in each section of the board.
- Hint #2: Find what blinds can go in a specific section. This can be done by choosing a section and checking each blind in this section.
- Hint #3: Determine the number of blank squares shown in the solution. The total number of squares that are visible on the board at any time is equal to the total number of 'holes' in each blind. In this case, there are 3 + 3 + 3 + 4 = 13 holes. To find the total number of visible blank squares, subtract the number of fruits which must be shown from the total number of visible squares (13). One can think of blanks as a separate kind of fruit and fill up the row of visible fruits above the board with them till one has 13.
- Hint #4: Count the number of each type of fruit that appears in the question. If a fruit doesn't appear in the question at all, then this means that every fruit of that type needs to be covered. You should also count the number of each type of fruit that appears on the board. This will help in case every fruit of the same type needs to be left visible.
- Hint #5: Start by trying to figure out where the purple blind should go. Since the purple blind is the only one which has its center open, figuring out where it can go on the board is easier, since the middle fruit of its section will always be visible. It is also a good idea to place the green blind last. Since it has eight states (as described below), it may save you some time if you wait to place this blind until the end.
- Hint #6: Use one hint to enable another. Even if a hint is not successful in placing a blind it may reduce the number of fruits which can be left by another blind. An example of this is if a question requires one apple to be visible, and a specific blind always reveals one apple. This means that no other blinds should show an apple, which makes it easier for one to place the other blinds. This is similar to the game Sudoku, where there may be some rule which won't fix the placement of a number but might limit the remaining options such that another rule is now successful.
- Hint #7: Flip only the green blind. As described further down, all blinds except the green one have a mirror symmetry. Therefore one can save time by not attempting to flip these three mirror symmetric blinds. Trying all their rotations is enough.
Some solutions with explanations.
-
The following examples will show that knowing the hints from the section above will help you solve all of the puzzles.
- First of all, this question wants us to only have six bananas showing. Using Hint #4, we can see that there are only six bananas in total on the board, and we know that all of them must be visible. We also know that all of the other types of fruit must be covered.
- Next, using Hint #5, we can see that there is a banana in the center of the top right section of the board. This means that the purple blind must go here, since it is the only blind which leaves the center visible. We can place the purple blind here and rotate it so that no other fruits are showing, and then move on.
- Now we can look at the bottom left section of the board. There are no bananas here, which means that every one of the fruits in this section must be covered with a blind. Using Hint #2 with the three remaining blinds, we can see that the green blind is the only one which covers all of these fruits.
- Now we can use Hint #1 on each of the two remaining blinds, starting with the blue blind. After doing this, we can see that it must go in the bottom right section, since it can never show all three bananas in the top left section. Then we place the pink blind into the final section, and rotate it to show all three bananas.
- Let's start by using Hint #5 to determine where the purple blind should go. Since the top right section has a banana in the center, and the bottom left section of the board has an orange in the center, the purple blind cannot go in either of these two sections. Next, if we use Hint #1, we can test the purple blind in the top left section and the bottom right section. Using Hint #4, we can see that there is always an apple which is left visible. This means that we can eliminate the apple from the fruits that need to be left visible, which simplifies the question.
- Now we can use Hint #1, we'll start with the pink blind first. Now that we know that we can't show any apples, we find that the only place where this blind can go is in the top right section.
- Next let's check the blue blind, by using Hint #1 again. The only place where this blind can go is in the bottom left section, since it reveals either bananas or oranges in the other two sections. Now we can see that both cherries are visible, and so we can eliminate them from the question for now.
- Now, we need to place the remaining two blinds such that all three of the remaining grapes are left visible. Using Hint #1, we can start with the green blind, and see that it must go in the bottom right section. Finally, we can place the purple blind back in the top left section, and we are done.
An Easy Question
-
Now that you know more about the game, and some strategies to solve questions, let's solve a Beginner puzzle. Click the button below to show the question.
Please give it a try and see how far you can get before checking the solution.
A More Difficult Question
-
Now, let's solve a question involving more than one type of fruit. Click the button below to show the question.
Please give it a try and see how far you can get before checking the solution.
What makes a Fruit Salad puzzle more difficult?
- A puzzle gets more difficult when there are more types of fruit which must be left uncovered. If there is a small variety of fruit, such as if you were only looking for bananas and grapes, you can start by finding out which placements of the blinds leave only these visible. This helps to decrease the number of possible placements, and so the puzzle is easier to solve.
- If there is more variety, it is more difficult to narrow down the places where a blind can be placed, and so the question is harder. This is why it is important to use the hints listed above, especially when trying to solve more difficult questions (see the difficult example above).
- Another thing which makes a Fruit Salad puzzle difficult is how many times you need to swap, rotate, or flip blinds to get the right answer. Each question on this webpage has a unique answer, which means that they all have their own set of moves which must be performed to get the right answer. These moves don't need to be done in any specific order, and some moves can be replaced with others (e.g. rotating a shape three times to the right is the same as rotating it once to the left). Questions which have a larger set of moves are more difficult since it will take longer to find the right answer.
How many of the blinds are symmetric?
-
A blind can have different types of symmetry, mirror symmetry and/or rotational symmetry. A blind is mirror symmetric if flipping the blind has the same effect as turning it a certain number of times. A blind is rotationally symmetric if each 90 degree rotation leaves the blind unchanged.
How many of the blinds in this game are mirror symmetric?
-
Three of the blinds in this game are mirror symmetric. The pink and purple blinds are symmetric along the diagonal, and the blue blind is symmetric along the horizontal. The green blind is not mirror symmetric. For this game, it doesn't matter where the symmetry axis is because one can rotate each blind.
How many of the blinds in this game are rotationally symmetric?
-
None of the blinds in this game are rotationally symmetric. Blinds that do have this kind of symmetry (but are not used in this game) include a straight line or an 'X' shape.
How many states does each blind have?
-
A blind with mirror symmetry has only four different states to check, so the pink, blue, and purple shapes each have four states. A blind that doesn't have mirror symmetry has eight different states to check. Since the green blind is the only one which isn't symmetric, it is the only blind with eight different states. You can check this by trying all clockwise rotations of each blind, and then flipping the blind and rotating it again.
How many different ways are there to place all four blinds onto the board?
-
When you start placing the blinds onto the board, you have 4 different spots to place the first blind, then 3 different spots for the second, 2 different spots for the third, and one remaining location for the final blind. This leaves us with 4 × 3 × 2 × 1 = 24 placements. This number can also be referred to as 4 factorial, or 4!.
The three symmetrical blinds can be rotated four different ways, as shown previously. This gives us a total of (4 × 4 × 4) × (4 × 3 × 2 × 1) = 1536 different placements so far.
Finally, since the green blind can be rotated eight different ways, we get a total of (8 × 4 × 4 × 4) × (4 × 3 × 2 × 1) = 12288 different placements for the blinds.
How many placements would there be if none of the blinds were symmetrical?
-
Then there would be a total of (8 × 8 × 8 × 8) × (4 × 3 × 2 × 1) = 98304 different placements for the blinds.
For 'n' blinds with symmetry and 'm' blinds without symmetry, find a formula to calculate the number of possible placements of the blinds.
-
Say that we want to find the total for a board with 20 symmetrical blinds and 5 asymmetrical blinds. Instead of writing out 20 4's and 5 8's as we were doing before, we can create a formula to simplify this calculation.
From the section above, we know that the number of states for a symmetrical blind is 4. We can also see that for any number of symmetrical blinds, the total number of placements is 4n, where 'n' is the number of symmetrical blinds.
Likewise, we know that the number of states for an asymmetrical blind is 8, and we get the total number of placements to be 8m, where 'm' is the number of asymmetrical blinds.
As before, to find the total number of ways that the blinds can be placed (without including rotations) onto the board, we use s!, with 's' being the number of blinds.
Multiplying these together gives us 4n × 8m × s! = t, where 't' is the total number of placements for the blinds.
Since 22 = 4 and 23 = 8, the formula can be simplified as follows:
4n * 8m = (22)n * (23)m
= (22n) * (23m)
= 22n + 3m
This gives us a final formula of 22n + 3m × s! = t, where 'n' is the number of symmetrical blinds, 'm' is the number of asymmetrical blinds, 's' is the total number of blinds (which can also be found with n + m), and 't' is the total number of placements for the blinds. Try this formula using the numbers for the board on this webpage (one asymmetrical blind and three symmetrical blinds).
Now that we know that the formula is correct, we can figure out the number of placements for the board described at the beginning of this section, with 20 symmetrical and 5 asymmetrical blinds.
22n + 3m * 25! = t
22(20) + 3(5) * 25! = t
240 + 15 * 25! = t
255 * 25! = t
5.59 x 1041 = t
(The exact answer is 558850238169687388730388679609024512000000, or five hundred and fifty-eight duodecillion, eight hundred and fifty undecillion, two hundred and thirty-eight decillion, one hundred and sixty-nine nonillion, six hundred and eighty-seven octillion, three hundred and eighty-eight septillion, seven hundred and thirty sextillion, three hundred and eighty-eight quintillion, six hundred and seventy-nine quadrillion, six hundred and nine trillion, twenty-four billion, five hundred and twelve million.)
Why would I need to know this?
-
While knowing how to find the number of placements doesn't help you solve the puzzles, it's still useful. While we were developing this game, we needed to make sure that each question only has one solution. To do this, we first had to find all of the possible placements for the board. To store these placements, we used an array, which has a fixed size. We used the formula above in order to determine what size the array should be.
More about the blinds.
-
The four blinds on the board are each made up of smaller squares. Three of them are made of six squares, and the other is made of five.
A shape which is made up of a number of smaller squares is called a Polymino. There are more specific terms for shapes with a specific number of squares. Hexominoes are made up of six squares, and Pentominoes are made up of five.
Many well-known games use polyminoes, including Tetris, Blokus, and Dominoes. There are also some versions of Sudoku which use polyminoes instead of squares for the grid.
More information about polyminoes can be found at:
Follow or subscribe for updates: